I WAS JUST LOOKING FOR AN EXAMPLE!

or
How I came to reacquaint myself with the fact that the altitudes of a triangle bisect the angles of its orthic triangle and other interesting facts about the orthic triangle.

Bill Richardson
Wichita State University

Some students in my geometry class were strugglinig with the concepts of cross ratio and harmonic division, so I went looking for some problems to work for them as examples of using these concepts. In Howard Eves' book, College Geometry, I found the following problem:

If $P,Q,R$ are the feet of the altitudes on the sides $BC, CA, AB$ of a triangle $ABC$, show that $P(QR,AB)=-1.$

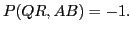
This sounded like a nice problem, but when I worked it in preparation for class, I discovered that I did not use the fact that $AP, BQ, CR$ were altitudes. The only property of altitudes that I used was the fact that the altitudes of a triangle are concurrent. Therefore my solution was valid for any concurrent cevian lines $AP, BQ, CR$. In fact I found two nice solutions. One based on the properties of Ceva's and Menelaus' theorems and the other using the properties of a complete quadrilateral.

After I completed these solutions, I looked at Eves' hint for the problem to see why he required the cevian lines to be altitudes. His hint was for the student to use the fact that the altitude $AP$ bisected the angle $QPR$. This certainly gave a solution, except for one minor point: nowhere in the book (that I could find) was this fact, or material relating to it, presented. I have a policy, in both my geometry course and my number theory course, that if a student uses a hint given by the author of the text, then the student must first prove the hint is valid before they can use it in their solution. I decided to see what was involved in writing up a proof for this fact that $AP$ bisects angle $QPR$. When I started working on this, I found that I was awakening distant memories about properties of the orthic triangle.

The Orthic Triangle

If AP, BQ, CR are the altitudes for a triangle ABC, the triangle formed by joining the feet of the altitudes P, Q, R, is called the orthic triangle for triangle ABC. (NOTE. Some call this the pedal triangle; however, in general, a pedal triangle for an acute triangle is the triangle formed by the feet of the projections of an interior point of the triangle onto the three sides. Hence there are an infinite number of pedal triangles for a given triangle.) When looking at the orthic triangle for a given triangle $ABC$ there are two cases to be considered: triangle $ABC$ is an acute triangle and triangle $ABC$ is an obtuse triangle.

Figure 1. The Two Cases

I will refer to triangle $ABC$ as the parent triangle. If the parent triangle is acute, then the altitudes of this triangle bisect the angles of its orthic triangle; however, if the parent triangle is obtuse, the angles of the orthic triangle are bisected by the two sides forming the obtuse angle and the altitude to the side opposite the obtuse angle. We will look at each case separately.

After this examination, we will show that the orthic triangle is the triangle with minimum perimeter for all triangles inscribe in a given triangle.

The Orthic Triangle for an Acute Triangle

Theorem. The altitudes AP, BQ, CR of an acute triangle ABC bisect the angles of its orthic triangle PQR.

Figure 2. The Orthic Triangle for an Acute Triangle

Proof. We will show that AP bisects $\angle QPR$ and the others will follow by similar arguments.

We begin by constructing circles $\Sigma_1,\ \Sigma_2,\ \Sigma_3$ on sides $AB,\ AC, \ BC$ as diameters.

Figure 3. $AP$ bisects $\angle RPQ$

Circle $\Sigma_1$ was constructed on AB as its diameter. This circle must pass through P and Q since triangles APB and AQB are right triangles on the same hypotenuse AB. In a like manner, $P$ and $R$ lie on circle $\Sigma_2$ and $Q$ and $R$ lie on cirle $\Sigma_3$. Since angles RPA and RCA subtend the same arc AR on circle $\Sigma_2$ we have that $\angle RPA = \angle RCA=\angle HCA$. Next, we see $\angle RBQ = \angle RCQ$, since the both subtend arc $RQ$ on circle $\Sigma_3$. Now $\angle APQ = \angle ABQ$ since they both subtend arc AR on $\Sigma_1$. Thus, we have

$$\angle RPA = \angle RCA = \angle QBA=\angle QPA$$    and $$\angle RPA = \angle QPA$$

which means AP bisects $\angle QPR$. By similar arguments, using circles $\Sigma_1,\ \Sigma_2,\ \Sigma_3$, we can show that BQ bisects $\angle PQR$ and CR bisects $\angle QRP$.

ADDENDUM. From the above discussion, we have some bonus properties. Since the altitudes of a triangle are concurrent and are the internal angle bisectors of the angles of the orthic triangle, we see that the orthocenter $H$ is the incenter for triangle $PQR$. If the altitudes of a triangle are the internal angle bisectors of the angles of the orthic triangle, then the sides are the external angle bisectors since the internal and external bisectors of an angle are perpendicular. We therefore have that the vertices $A, B, C$ are the centers for the excircles for the orthic triangle. This is illustrated in Figure 4. I vaguely remember mention of the orthic triangle when I was an undergraduate student but at that time I believe we only talked about the orthic triangle for an acute parent triangle. This got me curious about the case for the obtuse parent triangle. We examne this next.

Figure 4. The Incircle and Excircles for Triangle $RPQ$

The Orthic Triangle for an Obtuse Triangle

Theorem. Let $ABC$ be an obtuse triangle, angle $B$ the obtuse angle and let $AP$, $BQ$, $CR$ be the altitudes to the sides $BC, CA, AB$. Let triangle $PQR$ be the orthic triangle for triangle $ABC$. Then side $BC$, altitude $BQ$ and side $AB$ bisect the angles $P,Q,R$ of the orthic triangle. Furthermore, $B$ is the incenter for the orthic triangle.

Figure 5. The Orthic Triangle for an Obtuse Triangle

Proof. In Figure 5, $ABC$ is the given triangle and triangle $PQR$ is its orthic triangle.

We need to prove that $\angle RPB = \angle BPQ$, $\angle PQB = \angle BQR$ and $\angle PRB = \angle BRQ$. To this end we construct circles $\Sigma_1,\ \Sigma_2,\ \Sigma_3$ on sides $AB, BC, CA$ as diameters.

In Figure 6, we see that $\angle RPC = \angle RAC$ since they both subtend arc $RC$ on circle $\Sigma_3$. We also have that $\angle RAC=\angle BAQ=\angle BPQ$ since the subtend arc $BQ$ on circle $\Sigma_1$.Hence

$$\angle RPB = \angle RPC = \angle RAC = \angle BAQ=\angle BPQ$$

and $\angle RPB = \angle BPQ$ and therefore side $BC$ bisects angle $RPQ$.

Figure 6. $BC$ bisects $\angle QPR$

We next consider altitude $BQ$ and angle $PQR$. In Figure 7, $\angle PQB=\angle PAB$ since they both subtend arc $PB$ on circle $\Sigma_1$. In the middle part of Figure 3 we see that $\angle PAB = \angle PAR = \angle PCR$ since angles $PAR$ and $PCR$ subtend arc $PR$ on circle $\Sigma_3$. Now in the right-hand part of Figure 7, we see that $\angle PCR = \angle BCR = \angle BQR$ since angles $BCR$ and $BQR$ subtend arc $BR$ on circle $\Sigma_2$. Thus $\angle PQB=\angle PAB=\angle PCR=\angle BQR$ so that $\angle PQB = \angle BQR$ and altitude $BQ$ bisects angle $PQR$.

Figure 7. $BQ$ bisects $\angle PQR$

To finish, we need to show that side $AB$ bisects angle $PRQ$. In Figure 8 we see that $\angle PBR = \angle PRA=\angle PCA=\angle BCQ$ since angles $PRA$ and $PCA$ subtend arc $AP$ on circle $\Sigma_3$. Also $\angle BCQ = \angle BRQ$ since they subtend arc $BQ$ on circle $\Sigma_2$. Hence $\angle PRB = \angle BCQ = \angle BRQ$ and $\angle PRB = \angle BRQ$, which imples that $AB$ bisects angle $PRQ$.

Figure 8. $AB$ bisects $\angle PRQ$

Since the angle bisectors $BC, BQ, AB$ all meet in $B$, it is clear that $B$ is the incenter for the orthic triangle $PQR$.

Figure 9. The Incircle for the Orthic Triangle

As a final note, we see in Figure 10 that the vertices $A$ and $C$ and the orthocenter $H$ for triangle $ABC$ are the centers for the excircles of the orthic triangle $PQR$.

Figure 10. The Excircles for the Orthic Triangle

The Orthic Triangle for an Acute Triangle is the Inscribed Triangle with Minimum Perimeter

Theorem. For an acute triangle, the orthic triangle is the inscribed triangle with minimum perimeter.

Figure 11. An Inscribed Triangle for Acute Triangle $ABC$

Proof. Consider triangle $PQR$ inscribed in an acute triangle $ABC$. Reflect $P$ across $AB$ to get $P_1$ and reflect $P$ across $CA$ to get $P_2$. Since triangles $PP_1R$ and $PQP_2$ are isosceles, $RP_1=RP$    and $PQ = P_2Q$. Hence the polygonal path $P_1RQP_2$ is equal to the perimeter of triangle $PQR$. Now if we leave $P$ fixed and let $R$ and $Q$ move along $AB$ and $CA$ until they lie on line $P_1P_2$ (Figure 2), then the perimeter of triangle $PQR$ will equal $P_1P_2$.

Figure 12. $R$ and $Q$ on $P_1P_2$

Now since triangles $P_1AP$ and $P_2AP$ are isosceles, $AP_1=AP=AP_2$. Furthermore, $\angle P_1AP_2 = 2\angle A$, since $AB$ is the bisector of $\angle P_1AP$ and $AC$ is the bisector of $\angle PAP_2$.

Now with $R$ and $Q$ on line $P_1P_2$, if we now allow $P$ to move along $BC$, $\angle P_1AP_2$ will remain constant with measure the same as $2\angle A$. Triangle $P_1AP_2$ will always remain an isosceles triangle; however, its base $P_1P_2$ will vary in direct proportion to $AP$. Thus $P_1P_2$ will be a minimum when $AP$ is a minimum and that occurs when $AP$ is the altitude of triangle $ABC$ to side $BC$.

This process can be repeated for $Q$ and $R$ to show that they are the feet of the altitudes from $B$ and $C$. Therefore the triangle with minimum perimeter is the orthic triangle. See Figue 13.

Figure 13. The Orthic Triangle