Exercise. If
![]() are concurrent cevian lines for triangle
are concurrent cevian lines for triangle ![]() , show that
, show that
![]()
(Note. The following solutions require a knowledge of Ceva' and Menelaus' Theorems as well as knowledge of cross ratios, harmonic division and complete quadrilaterals.)
Solution 1. In the figure below extend ![]() to meet
to meet ![]() in
in ![]() . Let the cevian lines
. Let the cevian lines
![]() be concurrent on a point
be concurrent on a point ![]() .
.
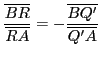 , or
, or
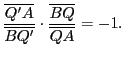 Thus,
Thus,
Solution 2. In the above figure, consider the quadrilateral ![]() . If we make this a complete quadrilateral, then
. If we make this a complete quadrilateral, then ![]() and
and ![]() are vertices and
are vertices and ![]() and
and ![]() are diagonal points. We know that on the diagonal line
are diagonal points. We know that on the diagonal line ![]() there is a harmonic range consisting of the two diagonal points and the two vertices lying on the diagonal line. Hence
there is a harmonic range consisting of the two diagonal points and the two vertices lying on the diagonal line. Hence
![]() . But
. But
![]() and it follows that
and it follows that
![]() .
.