M555: Ordinary Differential Equations

2.2 Separable Differential Equations

---

2.2.1 Separable Differential Equations

In this section, we will look at another type of first-order differential equation

$$ \dfrac{dy}{dx} = f(x,y) $$
that has a special form. Suppose that it is possible to write the function $f(x,y)$ as a product of two functions $g(x)$ and $h(y)$. This means that we may "separate" the variables $x$ and $y$:
$$ \dfrac{dy}{dx} = g(x)h(y). $$

In Section 1.2 , we showed how these are solved by integrating both sides with respect to the appropriate variable and finding an explicit formula for $y$ if possible.

2.2.2 Examples of Separable Equations

Example 1

Find the general solution to the differential equation

$$ y' = \cos^2(x)\cos^2(2y) $$

Follow Along

First, we separate variables:
$$ \sec^2(2y)y' = \cos^2(x).$$
This form is equivalent to
$$ \sec^2(2y)\,dy = \cos^2(x)\,dx $$
so we may integrate both sides with respect to the appropriate variables
$$ \int \sec^2(2y)\,dy = \int \cos^2(x)\,dx. $$
On the left, we have tangent, and the right requires the trigonometric identity $ \cos^2(x) = \frac{1}{2}\Big(1+\cos(2x)\Big) $,
$$ \frac{1}{2}\tan(2y) = \int \frac{1}{2}\Big(1+\cos(2x)\Big)\,dx = \frac{x}{2} + \frac{1}{4}\sin(2x) + C $$
Multiplying both sides by $2$ to simplify, we have
$$ \begin{aligned} \tan(2y) &= x + \frac{1}{2}\sin(2x) + C. \end{aligned} $$
The direction field for this looks like

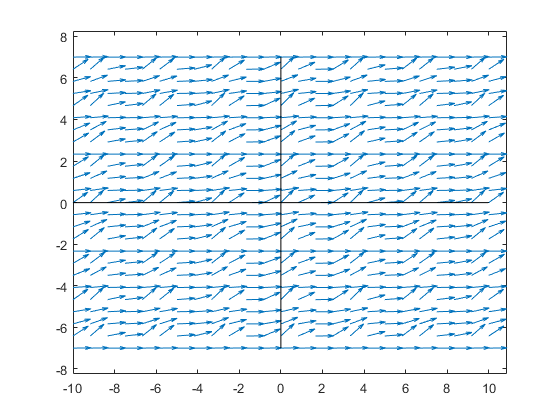
Example 2

Solve the initial value problem for

$$ y' = \dfrac{xy^3}{\sqrt{1+x^2}},\quad y(0) = 1 $$
and determine the interval in which the solution is defined.

Check Your Work

$$ y(x) = \sqrt{\dfrac{1}{3-2\sqrt{1+x^2}}}\qquad x\in\left(-\infty, \frac{\sqrt{5}}{2}\right) $$

Video Solution

2.2.3 Homogeneous Equations

Some equations may be expressed as a function of the ratio $\frac{y}{x}$ only. These equations are called homogeneous .
Equations of this type may always be transformed into a separable equation. Let's do an example to demonstrate the procedure for how to solve a first-order homogeneous equation.

$$ \dfrac{dy}{dx} = \dfrac{y-9x}{x-y} $$
First, we factor out an $x$ from both the numerator and denominator to get $\frac{y}{x}$.

$$ \dfrac{dy}{dx} = \dfrac{\frac{y}{x}-9}{1-\frac{y}{x}} $$
Next, we introduce new variable $v(x) = y(x)/x$. This allows us to rewrite our differential equation in terms of $x$, $v(x)$, and $\dfrac{dv}{dx}$. Making the necessary replacements,

$$ \dfrac{d}{dx}\left(xv\right) = \dfrac{v - 9}{1 - v}. $$
On the left hand side, it is necessary to use a product rule to compute the expression

$$ v + xv'(x) = \dfrac{v - 9}{1 - v}. $$
It is now possible to separate variables

$$ \begin{aligned} xv'(x) &= \dfrac{v - 9}{1 - v} - v \\ \\ &= \dfrac{v - 9}{1 - v} - \dfrac{v(1 - v)}{1 - v} \\ \\ &= \dfrac{v^2 - 9}{1-v} \\ \\ x\dfrac{dv}{dx} &= \dfrac{v^2 - 9}{1-v}. \end{aligned}$$
The $x$ and $v$ variables have been isolated on either side of the equation, but unfortunately they are on the "wrong" sides. After correcting this, we have

$$ \dfrac{1-v}{v^2 - 9}\, dv = \dfrac{1}{x}\, dx. $$
At this point, we will integrate both sides with respect to the appropriate variables. On the left hand side, this will require utilizing a partial fraction decomposition.

$$ \begin{aligned} \int \dfrac{1-v}{(v-3)(v+3)}\, dv &= \int \dfrac{A}{v-3} + \dfrac{B}{v+3}\, dv \\ \\ &= \int \dfrac{A(v+3)}{(v-3)(v+3)} + \dfrac{B(v-3)}{(v+3)(v+3)}\,dv\\ \\ &= \int \dfrac{v(A+B) + (3A - 3B)}{(v-3)(v+3)}\,dv \end{aligned} $$
This implies that $ 1-v = v(A+B) + (3A - 3B) $, and so we have the system of equations

$$ \begin{aligned} A + B &= -1 \\ \\ 3A - 3B &= 1. \end{aligned} $$
Solving this system yields $A = -\frac{1}{3}$ and $B = -\frac{2}{3}$, and our integral becomes


$$ \begin{aligned} \int \dfrac{1-v}{(v-3)(v+3)}\, dv &= \int \dfrac{-\frac{1}{3}}{v-3} + \dfrac{-\frac{2}{3}}{v+3}\, dv \\ \\ &= -\dfrac{1}{3}\ln|v-3| - \dfrac{2}{3}\ln|v+3| + C. \end{aligned} $$

Note on Integration Constants

When we are solving differential equations, we will often need to do many algebraic manipulations after integrating. These changes also affect any constants of integration that appear. However, it is very tedious to track all of the changes that happen to the constant. In practice, most of these changes are not explicitly tracked unless they change the form of the solution. This means that if you change the integration constant by a scalar through addition or multiplication those changes need not be tracked. However, if you multiply the integration constant by a variable or apply a function to it, you must write it down.

Combining this with the right hand side from our separated differential equation from above, we have that

$$ -\dfrac{1}{3}\ln|v-3| - \dfrac{2}{3}\ln|v+3| = \ln|x| + C, $$
which may be simplified by using logarithm properties

$$ \begin{aligned} \ln|v-3| + \ln|v+3|^2 &= -3\ln|x| + C \\ \\ \ln\left(|v-3|(v+3)^2\right) + \ln|x|^3 &= C \\ \\ \ln\left(|x|^2|v-3|(v+3)^2\right) &= C \\ \end{aligned} $$
and by applying the exponential function to both sides

$$ |x|^3|v-3|(v+3)^2 = C. $$
At this point we recognize that the real fixed but arbitrary value $C$ can be utilized to remove the absolute value symbols. If the product is positive then $C$ is positive. If the product on the left is negative then $C$ is negative. So

$$ x^3(v-3)(v+3)^2 = C. $$
Lastly, we need to return to our original variables, so we replace $v$ with $\frac{y}{x}$ and simplify

$$ \begin{aligned} x^3\left(\frac{y}{x}-3\right)\left(\frac{y}{x}+3\right)^2 &= C \\ \\ (y-3x)(y+3x)^2 &= C. \end{aligned} $$
Since it is not clear how to isolate the variable $y$ in this expression, we arrange it like this to be able to investigate the direction field.

2.2.4 Drawing the Direction Field with Python

Below is a Python program that generates a direction field for Exercise 2.2.3 . Python is an open source programming language that has seen a recent explosion in its popularity for computational mathematics and is one of the tools that you may encounter in your other courses. It is not required for this course and only included as an example. If would like to learn more, there are many tutorials available via web search. If we consider an initial condition

$$ y(0) = y_0, $$
then we can compute our arbitrary constant.

$$ (y_0 - 0)(y_0 + 0)^2 = y_0^3 = C. $$
Our solution becomes

$$ (y - 3x)(y + 3x)^2 = y_0^3 $$
For our example

$$ \dfrac{dy}{dx} = \dfrac{y-9x}{x-y}, $$
the direction field shows a gap at $y=x$, since the derivative is not defined for those values. Integral curves are graphs of solutions for various values for $y_0$. The green integral curves are graphs of solutions for positive values of $y_0$; and the purple integral curves are graphs of solutions for negative values of $y_0$.

import numpy as np
import matplotlib.pyplot as plt
import warnings

# Suppress warnings (we're going to have stuff that looks like we're dividing by 0)
warnings.simplefilter("ignore")
# Differential equation
def diff(x,y):
    v = (y-9*x)/(x-y)
    v = np.nan_to_num(v) # converts nan (not a number) to 0
    DX = 1/np.sqrt(1+np.power(v,2))
    DY = v/np.sqrt(1+np.power(v,2))
    return DX, DY
# Generate grid points for figure
x = np.linspace(-10,10,50)
y = np.linspace(-10,10,50)
X1 , Y1 = np.meshgrid(x,y)
# Calculate growth rate at each grid point
DX1, DY1 = diff(X1, Y1)
M = (np.hypot(DX1, DY1))
# This is to avoid any divisions by 0 when normalizing
M[ M == 0] = 1.
# Normalize the length of each arrow (optional)
DX1 /= M
DY1 /= M
# Plot the figure
plt.figure(figsize=(13,13))
plt.quiver(X1, Y1, DX1, DY1, color='blue', units='xy', scale=5., 
               zorder=3, width=0.03, headwidth=3., headlength=4, pivot='mid')
plt.title(r"Slope field $y'= \dfrac{y-9x}{x-y}$")
plt.grid(True)
plt.show()