|
50,000 B.C.E.
|
|
Evidence of counting
|
50,000 B.C.E.
|
|
Neanderthal man
|
|
25,000 B.C.E.
|
|
Primitive geometrical designs
|
25,000 B.C.E.
|
|
Paleolithic art: Cro-Magnon man
|
|
|
|
|
4000 B.C.E.
|
|
Use of metals
|
|
|
|
|
3500 B.C.E.
|
|
Writing
|
|
3000 B.C.E.
|
|
Hieroglyphic numerals
in Egypt
Hieroglyphics for numbers were introduced around 3000 BCE. The number
glyphs were: a stroke, or staff,  for one; a heel bone
for one; a heel bone 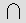 for 10; a
coil of rope for 10; a
coil of rope 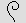 for 100; a lotus
flower for 100; a lotus
flower  for 1000; a pointing
finger for 1000; a pointing
finger 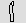 for 10,000; a
borbot fish (or tadpole) for 10,000; a
borbot fish (or tadpole) 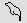 for 100,000; and an astonished man
for 100,000; and an astonished man 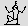 for 1,000,000. Clearly their number system was a base ten
system; however, they used a simple grouping system rather than a
positional system. for 1,000,000. Clearly their number system was a base ten
system; however, they used a simple grouping system rather than a
positional system.
|
3000 B.C.E.
|
|
Use of wheeled vehiclesWheeled
vehicles first appeared in Mesopotamia (the region between the Tigris
and the Euphrates Rivers ) around 3000 B.C.E. They were originally
four-wheel vehicles drawn by slow-moving animals. The wheels on the
earliest vehicles were fixed to the axles rather than rotating around a
hub. The axles themselves were held in place with wooden pegs on each
side of the axle. The axle rotated against the bed of the vehicle and
this probably helped round the axles.
|
|
2773 B.C.E.
|
|
Likely introduction of the Egyptian calendar
(Some hypothesize 4241 B.C.E. as the origin.)
|
|
|
|
|
|
|
|
2500 B.C.E.
|
|
Great PyramidThe
Great Pyramid was built by the Egyptian pharaoh Khufu (also known as
Cheops) of the Fourth Dynasty around the year 2500 BCE to serve
as a tomb for when he died. This pyramid is believed to have been built
over a 20-30 year period and it is the only survivor of the Seven
Wonders of the Ancient World. It is properly referred to as the Great
Pyramid of Giza. The site was first prepared by leveling the surface
and then blocks of stone were transported and placed. It was finished
with an outer casing which was used to smooth the surface. This outer
surface has long ago disappeared.
Some interesting data: it is 756 feet long on each side, 480 feet high
and is composed of approximately 2,300,000 blocks of stone, each
averaging 2 1/2 tons in weight. Despite the limited surveying tools of
the time, it is reported that no side is more than 8 inches different
in length than another. Furthermore, the whole structure is perfectly
oriented to the points of the compass. For about 4500 years it was the
tallest building in the world. It was not surpassed until the 19th
Century.
There is much speculation on exactly how this pyramid and its
companions were actually constructed.
|
|
2400 B.C.E.
|
|
Positional notation for
numbers in Mesopotamia Around 2400 B.C.E. the Sumerians
developed the sexagesimal
system. This is a positional number system based on sixty, rather than
ten. The Sumerians represented the integers using cuneiform wedge
patterns. Their writing material consisted of a stylus and a tablet of
soft clay which, when completed, was allowed to harden into a permanent
document. They used a vertical wedge to represent a unit and a sidewys
wedge to represent ten units. With arrangements of these two symbols
they could represnt numbers of any size. Numbers between 1 and 59 were
the symbols for 1 and 10 tightly grouped together. When these "digits"
were to multiply powers of 60, they were separated by more space. If
the Sumerians wanted to represent our number 10,884, they would put
three closely spaced vertical wedges followed by a space and then one
vertical wedge followed by a space and finally two sideways wedges and
four vertical wedges closely spaced to each other. This represented 3(602)
+ 1(60) + 24 (using our notation).
|
2400 B.C.E.
|
|
Sumerian-Akkadian Empire
|
|
1850 B.C.E.
|
|
Moscow Papyrus:
arithmeticThe Moscow Papyrus is located in the Museum of Fine
Arts in Moscow whence its name. This papyrus was copied by an unknown
scribe (around 1850 B.C.E.). It was brought to Russia during the middle
of the 19th century. It contains 25 mathematics problems
involving simple “equations” and solutions. Of course the equations are
not in modern form. The problem that generates the most interest is the
calculation of the volume of a truncated pyramid (a square based
pyramid with the top portion removed). The Egyptians seemed to know the
formula for this even though this is a difficult formula to derive.
|
|
|
|
|
|
|
|
1800 B.C.E.
|
|
Code of Hammurabi
|
|
|
|
|
1700 B.C.E.
|
|
Stonehenge in England
|
|
1650 B.C.E.
|
|
Rhind PapyrusThe
Rhind Papyrus (AKA the Ahmes Papyrus) is named after the Scottish
collector, Henry Rhind, who acquired it in 1858. It evidently was a
copy of a copy. It was copied by a scribe, Ahmes (around 1650 B.C.E.)
who claimed it was obtained from another document written about 2000
B.C.E. This document was possibly copied from another document dating
to around 2650 B.C.E. The Rhind Papyrus is located in the British
Museum. This document is one of the primary sources of early Egyptian
mathematics. It contains over 80 problems and solutions as well as a
table of decomposition of fractions of the form 2/n.
Ahmes may well be the earliest “named” person in the history of
mathematics.
|
|
|
|
|
|
|
|
1400 B.C.E.
|
|
Catastrophe in
Crete-fall of the Minoan Civilization Catastrophe in Crete
(Three dates are reported: 1380, 1450,
1628 B.C.E.)
Around 1400 B.C.E., a natural catastrophe occurred in the area around
Crete which, according to the famous Greek archaeologist Spyridon
Marinatos, eventually led to the collapse of the mighty Minoan
civilization. Modern geological research has proved this theory to be
correct. The catastrophe was the eruption, and resulting tsunamis, of
the Satorini Volcano (also known as Thera) in the Aegean Sea. This
eruption is considered to be one of the largest in the last 10,000
years and is the probable cause of the end of the Minoan civilization.
(Legend has it that this Minoan civilization is the lost civilization
of Atlantis!)
|
|
|
|
|
1350 B.C.E.
|
|
Use of iron: sundials: water clocks
|
|
|
|
|
1200 B.C.E.
|
|
Trojan war
|
|
|
|
|
776 B.C.E.
|
|
First Olympiad
|
|
|
|
|
753 B.C.E.
|
|
Founding of RomeThe
Founding of Rome is very much embroiled in the myth involving Romulus
and Remus and Aeneas. It appears that rather than contradict each
other, the tale of Aeneas adds to that of Romulus and Remus.
Archaeological evidence shows that early settlement of the Palatine
Hill dates back to about 750 B.C.E. This agrees very closely to the
established legend that Rome was founded on 21 April 753 B.C.E. This
date has been traditionally celebrated in Rome with the festival of
Parilia.
|
|
|
|
|
740 B.C.E.
|
|
Works of Homer and Hesoid
|
|
|
|
|
586 B.C.E.
|
|
Babylonia captivity
|
|
585 B.C.E.
|
|
Thales of Miletus –
deductive geometryThales of Miletus (624 – 547 B.C.E.)
Thales seems to be the first known Greek mathematician and philosopher.
He is often referred to as one of the Seven Sages of antiquity. He is
also credited by some historians with being the “Father of deductive
geometry.” Thales is usually credited with five theorems of elementary
geometry:
A circle is bisected by any diameter.
The base angles of an isosceles triangle are equal.
The angles between two intersecting straight lines are equal.
Two triangles are congruent if they have two angles and one side equal.
An angle in a semicircle is a right angle.
|
|
|
|
|
518 B.C.E.
|
|
Pythagorean arithmetic
and geometryPythagoras of Samos (569 – 475 B.C.E.)
Around 518 B.C.E. Pythagoras founded a philosophical and religious
school in Croton (now Crotone, in southern Italy) that had many
followers. (Pythagoras had started an earlier school in Samos which he
abandoned.) Pythagoras was the leader of a Society (Brotherhood) which
included an inner circle of followers known as mathematikoi. The
mathematikoi lived permanently with the Society, had no personal
possessions and were vegetarians. They were taught by Pythagoras
himself and obeyed strict rules set down by Pythagoras. All knowledge
and discoveries were attributed to Pythagoras. The rule that probably
had the most impact on the history of mathematics was that all members
of the brotherhood should observe strict loyalty to Pythagoras and the
brotherhood and maintain secrecy. All of what we know of Pythagoras and
his followers come from commentators who lived a hundred years of more
later, since it appears that all knowledge and information was passed
on orally.
What has become evident is that Pythagoras and his followers were
considered to be, among other things, pure mathematicians. Much of the
early Greek arithmetic and geometry can be traced back to the
Pythagoreans.
|
|
|
|
|
|
|
|
538 B.C.E.
|
|
Persians took BabylonIn
538 B.C.E. (some historians claim 539 B.C.E.), the Persians, under the
leadership of King Cyrus, took Babylon, the ancient capital of a
middle eastern empire covering modern Iraq, Syria, Lebanon, and Israel,
and
thus became masters of Western Asia. A remarkable aspect of the capture
of Babylon is the fact that Cyrus allowed the Jews (who were exiled in
Babylonia) to return home. This empire lasted for over two centuries
until it
was divided by the successors of Alexander the Great.
|
|
|
|
|
480 B.C.E.
|
|
Battle of Thermopylae
|
|
|
|
|
461 B.C.E.
|
|
Beginning of the Age of Pericles
|
|
450 B.C.E.
|
|
Parmenides' spherical
earthParmenides of Elia (ca. 515 - about 450 B.C.E.)
Parmenides was Greek philosopher who was a follower of Pythagoras. He
was an early believer of a cosmology that consisted of a spherical
earth and a finite, motionless, spherical universe.
|
|
|
|
|
430 B.C.E.
|
|
Death of ZenoZeno
of Elea (ca. 490 – ca 430 B.C.E.)
Zeno was an Eleatic philosopher and was a favorite disciple of
Parmenides. Philosophers of his time considered his philosophy to be
quite negative. Zeno wrote a book that reportedly contained forty
paradoxes concerning the continuum. Four of the paradoxes were to have
a significant impact on the development of mathematics. An interesting
discussion of these can be found at
http://plato.stanford.edu/entries/paradox-zeno/
:
Elements of Hippocrates
of ChiosHippocrates of Chios (470 – 410 B.C.E.)
Hippocrates of Chios was an excellent geometer who taught in Athens. He
worked on the problems of squaring the circle and duplicating the cube.
While working on the problem of squaring the circle, he was able to
find the areas of lunes. An interesting account of his quadrature
(squaring) of the lune can be found in
Journey Through Genius: The Great Theorems of Mathematics
by William Dunham
Hippocrates was the first to write an Elements of Geometry
and although his work is no longer extant it has been reported by later
Greek writers to have contained much of what Euclid included in his
first two books of the Elements, which appeared about 120 years later.
|
430 B.C.E.
|
|
Hippocrates of Cos (the Physician)
Hippocrates of Cos (460 – 357 B.C.E.)
Hippocrates of Cos is known to us as the Father of Western Medicine and he is
credited with originating the Hippocratic Oath that all doctors take upon completing
their studies. The modern oath is quite close to the original.
|
|
|
|
|
429 B.C.E.
|
|
Death of PericlesPERICLES
(495?-429 B.C .E)
Under the leadership of the statesman Pericles, Greece reached the
height of its glory in the 5th century BCE. Pericles was born to a
family of wealth and position. Among his accomplishments was to bring
the ordinary citizen into the Athenian democracy. He was a gifted
orator as was documented by the historian Thycidides. Pericles was
credited with creating the mighty Athenian empire. The fear of the
power of this empire by Sparta lead to the Peloponnesian War and while
Athens was besieged by the enemy outside the walls, a terrible plague
raged within. All these troubles caused Pericles to lose his popular
support and he was deposed from office; however, a few weeks later the
people repented and he was reinstated with greater powers than before.
He finally died from the after effects of the plague.:
The plague at AthensTHE PLAGUE IN
ATHENS DURING THE PELOPONNESIAN WAR
The plague in Athens was caused by the war strategy of Pericles. His
strategy was to bring all citizens from the surrounding area into
Athens and let the Spartans have control of the outlying area. He
planned on having Athens supplied with essential food and necessities
by the navy. However, he did not count on the overcrowding in the city
causing a disastrous plague.
|
|
427 B.C.E.
|
|
Birth of Plato
|
|
|
|
|
420 B.C.E.
|
|
Quadratrix (Trisectrix)
of HippiasHippias of Elis (460 B.C.E. - 400 B.C.E. dates are
approximates)
Hippias was knowledgeable in many areas. His major contribution to
mathematics was the quadratrix (also called the trisectrix) which he
reportedly used for trisecting an angle and squaring the circle. The
curve may be used for dividing an angle into any number of equal parts.
It appears that this was the first curve in in mathematics that was not
either a straight line or part of a circle. A definition and graph of
this curve can be found in the book A History of Pi by Petr
Beckmann.
|
|
|
|
|
|
|
|
404 B.C.E.
|
|
End of Peloponnesian WarThe
Peloponnesian War (431 – 404 B.C.E.)
This was a war between Athens and the Athenian empire versus
Sparta, Thebes, Corinth, and other members of the Peloponnesian
Confederacy. This war involved heavy fighting from Sicily to the coast
of Asia Minor and from the Hellespont and Thrace to Rhodes. It was the
first war in history to be recorded by an eyewitness historian,
Thycidides. According to Thycidides the cause of the war was Sparta's
fear of the growth of the power of Athens.
|
|
|
|
|
399 B.C.E.
|
|
Death of SocratesSocrates
(469-399 B.C.E.)
Socrates set the standard for all Western philosophy. Like
the mathematician Pythagoras, Socrates left no literary legacy of his
own. All we know of Socrates comes from others writing about his life
and work. In his early years Socrates showed a great deal of interest
in science, but he abandoned science to investigate the development of
moral character. Socrates served, with distinction, as a soldier in the
Peloponnesian War and after the war he worked as a stonemason. After
his father's death Socrates used the money he inherited to devoting all
his time to inventing the practice of philosophical dialog. In doing so
he became a controversial political figure and he was charged with
corrupting the youth of the city and interfering with the religion of
the city. For this he was sentenced to death. Socrates drank hemlock
and died in the company of his friends and disciples.
|
|
360 B.C.E.
|
|
Eudoxus' method of
exhaustionEudoxus of Cnidos (408?--355? BCE)
Eudoxus was the first to employ the method of exhaustion in
geometric proofs, a method that later geometers would return to again
and again. The basic idea is structured like an indirect proof. For
example, to show that region A has the same area as region B one could
proceed as follows: first one shows that the assumption that Area A
< Area B leads to a contradiction; next one shows that the
assumption that Area A > Area B leads to a contradiction.
Since neither of these is true, one is left with the fact that the only
remaining possibility, Area A = Area B, must be true.
|
|
|
|
|
350 B.C.E.
|
|
Birth of EudemusEudemus
of Rhodes (350 B.C.E. - 290 B.C.E.)
A course in the history of mathematics cannot overlook Eudemus of
Rhodes for he seems to have been the first major historian of
mathematics. Eudemus was not considered to be a producer of original
mathematics; however, he did write an original mathematical work called
On the Angle. This work is lost so we are unable to
judge its
importance but most historians consider it to be less important than
his contributions to the recording of the history of mathematics.
There were three works on the history of mathematics by Eudemus;
namely, History of Arithmetic, History of Geometry,
and History of Astronomy.
The History of Geometry is considered the most important
of the three mathematical histories of Eudemus. Even though the work is
not extant, it was available to many later writers who cited it
heavily.
|
|
|
|
|
332 B.C.E.
|
|
Alexandria foundedThe
city of Alexandria was the dream of Alexander the Great. He wanted to
create a cosmopolitan city that would be a center of commerce, culture
and knowledge. Alexander died before he could see the end result.
However, under the rule of the Ptolemys, Alexandria flourished and
became the city of Alexander's dreams. The Museum and Library drew
scholars from all over the known world. Almost every major
mathematician of the period spent time in Alexandria. Those who didn't
spend time there likely corresponded with the scholars who were there.
|
|
|
|
|
|
|
|
323 B.C.E.
|
|
Death of AlexanderAlexander
the Great (356 - 323 B.C.E.)
Alexander's parents wanted the best for their son, so they employed
some of the finest scholars around to educate him. When Alexander was
thirteen, he was tutored by the great Greek philosopher, Aristotle.
From him he learned the ways of the Greeks which influenced his life
from that point on. Alexander had great character and values and these
were two of the things that made Alexander the Great a prominent
individual in history. Another being that he was a great military
leader that allowed him to conquer a very vast amount of territory in a
relatively short amount of time.
Alexander died of mysterious causes and with no successor named on his
death bed, his empire went out to generals and officers who would then
become governors of sections of his empire. It was not long after that
that Alexander the Great's fractured empire crumbled.
It was one of Alexander's desires that a great cosmopolitan city be
built, and thus Alexandria came into existence.
|
|
|
|
|
322 B.C.E.
|
|
Death of Aristotle
|
|
|
|
|
305 B.C.E.
|
|
Ptolemy I (Soter) of
EgyptPtolemy I Soter (c.367- 283 B.C.E.)
Ptolemy I Soter was King of Egypt from 305 until 285 B.C.E. and founder
of the Ptolemaic dynasty. He was responsible for much of the greatness
of Alexandria, even though much of the work was completed by his son,
Ptolemy II. It was Ptolemy I who began the construction of the Pharos
Lighthouse in Alexandria, which was completed after his death. He also
was responsible for the erection of the great Mouseion, Alexandria's
famous ancient university. It was also Ptolemy I who created the famous
Library of Alexandria, and filled it with the books that would attract
great scholars to Egypt. In addition, it was Ptolemy I who was
responsible for having the Hebrew Bible translated into the Greek
language. Ptolemy I not only supported and encouraged the intellectual
infrastructure of Alexandria, he was also a scholar himself, for he
wrote a history of Alexander the Great.
|
|
300 B.C.E.
|
|
Euclid's ElementsEuclid
of Alexandria (ca. 325 B.C.E. - ca. 265 B.C.E.)
Little is known of Euclid of Alexandria's life except that he taught at
Alexandria. He is probably the most famous mathematician of antiquity
because of his being the author of the 13 books of The Elements.
To
this day there are still mathematicians who quote from The Elements.
This must make Euclid by far the leading mathematics teacher of all
time. The Elements are most often thought of in terms of geometry;
however, Euclid presented material on most of the known mathematics of
his time.
|
|
|
|
|
|
|
|
280 B.C.E.
|
|
Pharos, Lighthouse of
AlexandriaThe Pharos (Lighthouse of Alexandria) was built around
280 B.C.E. on the ancient island of Pharos in the harbor of Alexandria,
Egypt. It was approximately 400 feet high and it guided sailors for
about 1500 years. It has been classified as one of the Seven Wonders of
the Ancient World. It was destroyed by an earthquake in the 14th
century C.E.
|
|
|
|
|
264 B.C.E.
|
|
First Punic War
|
|
260 B.C.E.
|
|
Aristarchus'
heliocentric astronomyAristarchus of Samos (ca. 310 B.C.E. - 230
B.C.E.)
Aristarchus was a mathematician and astronomer and is best known as the
first to propose a sun-centered (heliocentric) universe. Nicolaus
Copernicus, in the mid 15th century, revived and acknowledged
Aristarchus's heliocentric concept. Aristarchus also gave his
calculations for the sizes and distances of the sun and moon.
|
|
|
|
|
230 B.C.E.
|
|
Sieve of EratosthenesEratosthenes
of Cyrene (276 B.C.E. - 194 B.C.E.)
In about 240 B.C.E., Eratosthenes became the third librarian at
Alexandria.
Although Eratosthenes was very knowledgeable in many areas, he was not
considered to be the top scholar in any one field. Some claim he earned
a nickname of “Beta” for this distinction—meaning that he was second
best in all fields. One of the areas that Eratosthenes worked in was
number theory, in particular the study of prime numbers. He is
well-known for his prime number sieve, the “Sieve of Eratosthenes”
which is still an important tool in number theory research. With this
sieve it is possible to sift the prime numbers out of the set of
positive integers with minimal computations.
Eratosthenes is credited with having made a surprisingly accurate
measurement of the circumference of the Earth. An interesting point to
ponder is that when Columbus decided to sail West to reach India he
supposedly thought that the circumference of the Earth was about 17,000
miles—about 7,000 miles short of the actual value. Would he have
ventured out in his three little boats if he had a more accurate value
for the circumference of the Earth?
|
|
|
|
|
225 B.C.E.
|
|
Conics of ApolloniusApollonius
of Perga (262 B.C.E. - 190 B.C.E.)
Apollonius of Perga was given the nickname “The Great Geometer”. He is
most remembered for his book Conics (about the conic
sections, curves that are created by slicing through a double cone with
a plane), in which he introduced the terms parabola, ellipse and
hyperbola. The Greek studies of conics are all the more remarkable when
one realizes that they did not have the advantages of a coordinate
system nor the tools of algebra that we use today.
|
|
|
|
|
212 B.C.E.
|
|
Death of ArchimedesArchimedes
of Syracuse (287 B.C.E. - 212 B.C.E.)
Archimedes is considered to be one of the all-time great mathematicians
and inventors. Even though he resided in Syracuse, Sicily, he is
considered to be an Alexandrian scholar. He corresponded with many of
the scholars in Alexandria.
There are many references to Archimedes in the writings of the time.
This was remarkable since his reputation was not gained after the fact,
which was most common for that time period. Much of his reputation came
about from his inventions. At the end of his life Syracuse was under
siege by the Romans under the leadership of Marcellus. Archimedes had
invented many machines which were used as engines of war that
frustrated the attacking Romans.
Although Archimedes gained great fame from his mechanical inventions,
he believed that pure mathematics was the only worthy pursuit. In fact,
he believed that a result was not truly established until a geometric
proof was supplied. Archimedes would devise a solution to a problem and
then transform it into a geometrical solution.
Archimedes was killed by a Roman soldier when the Romans finally
succeeded in gaining access to the city of Syracuse after many years of
frustration. Plutarch (a Greek historian) gave three different accounts
of the death of Archimedes. All seem to indicate that he was busy with
mathematical pursuits.
|
|
|
|
|
|
|
|
210 B.C.E.
|
|
Great Wall of China begunThe
Great Wall was originally built as a defensive fortification by the
three states: Yan, Zhao and Qin. The Great Wall actually began as
independent walls for different states when it was first built. It did
not become the "Great Wall” until the Qin Dynasty. Emperor Qin Shihuang
succeeded in his effort to have the walls joined together to fend off
the invasions from the Huns in the north after the unification of
China. The wall is approximately 4200 miles long and some sections are
in ruins and some parts have totally disappeared. However, it is still
observable by astronauts in space.
|
|
150 B.C.E.
|
|
360 degree circleAlthough Aristarchus
of Samos (ca. 310-230 B.C.E.) and Hipparchus of Rhodes (190 - 120 B.C.E.) both considered 360
equal parts in a circle, it was Hypsicles of Alexandria (ca. 190 - ca. 120 B.C.E.) who
named these parts as "degrees" when he divided the Zodiac into 360 degrees.
|
|
|
|
|
|
|
|
146 B.C.E.
|
|
Destruction of Carthage
|
|
140 B.C.E.
|
|
Trigonometry of
HipparchusHipparchus of Rhodes (190 B.C.E. - 120 B.C.E.)
Although Hipparchus was a mathematician and astronomer of major
importance, we have very few definite details of his work. The majority
of the information which we have about the work of Hipparchus comes
from Ptolemy's Almagest. Hipparchus was one of the few Greek
mathematicians to develop the mathematics leading to what we now call
trigonometry. He made many valuable contributions in this area that
were made use of by astronomers, like Ptolemy.
His early contribution to trigonometry was the creation of a table of
chords. This table would be considered as an early example of a
trigonometric table (something that those studying trigonometry after
the advent of the calculator may not be familiar with). Mathematical
historians often say that trigonometry was invented by him. The purpose
of this table of chords was to give a method for solving triangles in a
faster way than the traditional methods. Hipparchus is also credited
with introducing the division of a circle into 360 degrees into Greek
mathematics.
|
|
|
|
|
75 B.C.E.
|
|
Cicero restored tomb of
ArchimedesArchimedes' tomb was inscribed, according to his
wishes, with his favorite geometric theorem concerning the relationship
between a sphere and its circumscribed cylinder. The location of the
tomb was lost in the ensuing years; however, in 75 B.C.E. Cicero
discovered the forgotten and neglected tomb and he restored the burial
site of Archimedes.
|
.
|
|
|
|
|
|
|
44 B.C.E.
|
|
Death of Julius Caesar
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
60 C.E.
|
|
Geminus on the parallel
postulateGeminus (10 B.C.E. - 60 C.E.)
Geminus's mathematics text Theory of Mathematics is now lost but
information about it is available from a number of sources. Proclus,
Eutocius and Heron all cite this work. Proclus relies very heavily on
the work of Geminus when he writes his own history of mathematics and
it appears that Geminus' books are the most valuable sources available
to him.
Geminus is one of the early critics of the postulates of Euclid. In his
work he redefines parallel lines and gives an ingenious but false proof
for the parallel postulate. It is the earliest known attempt to proving
the Fifth Postulate as a Theorem. His fallacy was that he he assumed
that the locus of points at a fixed distance from a straight line is
itself a straight line and this cannot be proved without a further
postulate.
|
|
|
|
|
75 C.E.
|
|
Works of Heron of Alexandria
|
|
|
|
|
100 C.E.
|
|
Menelaus' Spherica
|
|
|
|
|
|
|
|
122 C.E.
|
|
Hadrian's Wall in
Britain begunThe first invasion of Britain by Rome occurred in 55
B.C.E. at the time of Julus Ceasar. At the time, the British Isles,
like much of mainland Europe was inhabited by many Celtic tribes
loosely united by a similar language and culture but not united in the
political sense. Over the years the Romans gained control over the
southern portion of the British Isles; namely, what is now England and
Wales. However the north remained under the control of what the Romans
considered “the barbarians.”
In 117 C.E. Hadrian became Emperor and at this time the Roman Empire
had
ceased to expand. Hadrian was concerned with maintaining his
boundaries. He visited Britain in 122 C.E., and ordered a wall to be
built between the Solway Firth in the West and the River Tyne in the
east "to separate Romans from Barbarians".
|
|
150 C.E.
|
|
Ptolemy's AlmagestClaudius
Ptolemy (85 C.E. - 165 C.E.)
Claudius Ptolemy's name is a mix of cultures. His first name "Claudius"
indicates that he was a Roman citizen, whereas "Ptolemy" was the name
of the Greek kings of Egypt, originally installed by Alexander the
Great. Ptolemy put together a work he called simply Mathematical
Compilation. This was an encyclopedia of everything that was known
at the time about astronomy. Some was original work by Ptolemy and some
was collected from other sources. It gave a means of calculating the
movements of the planets and was surprisingly accurate considering
Ptolemy used the Earth as the center of the universe. When the Arabs
found this work they called it Almagest, meaning “the
greatest.” Until the work of Copernicus in 1542, Almagest was
the primary source of astronomical knowledge.
|
|
|
|
|
|
|
|
180 C.E.
|
|
Death of Marcus Aurelius
|
|
250 C.E.
|
|
Diophantus' ArithmeticaDiophantus
of Alexandria (ca. 200 C.E. – ca. 284 C.E.)
Diophantus, is often referred to, falsely, as the “father of algebra”
and is best known for his Arithmetica, which contains
solutions of algebraic equations and material on the theory of numbers.
Arithmetica contains a collection of indeterminate
problems which mathematicians have named “Diophantine equations,” in
his honor. It was a Latin translation of this book by Bachet in 1621
that is most famous. Fermat used this edition and his study of the
material gave rise to the famous Fermat's Last Theorem.
|
|
|
|
|
320 C.E.
|
|
Pappus' Mathematical Collections
|
|
|
|
|
|
|
|
324 C.E.
|
|
Founding of Constantinople
|
|
405 C.E.
|
|
Death of Theon of
AlexandriaTheon of Alexandria (ca. 335 C.E. - 405 C.E.)
Theon of Alexandria worked in Alexandria as a teacher of mathematics
and astronomy. Probably his most notable work was the writing of an
important edition of Euclid's Elements, which is probably the version
that most modern writings on the Elements is based. Theon was the
father of Hypatia, considered to be the first female mathematician of
note.
|
|
|
|
|
415 C.E.
|
|
Death of HypatiaHypatia
of Alexandria (370 C.E. - 415 C.E.)
Hypatia of Alexandria is considered to be the first woman to make any
substantial contributions to the development of mathematics. She was
the daughter of Theon of Alexandria, who was a mathematician and
philosopher. In about 400 C.E. she became head of the Platonist school
at Alexandria where she lectured on mathematics and philosophy.
Although there is no evidence that she wrote any original mathematics,
Hypatia helped her father write a new version of the Elements
of Euclid
and she assisted him in his eleven part commentary on Ptolemy's Almagest.
She was quite proficient in mathematics and
astronomy.
Hypatia was murdered in 415 C.E. by Christians who felt threatened by
her
scholarship, learning, and depth of scientific knowledge.
|
|
|
|
|
|
|
|
455 C.E.
|
|
Vandals sack Rome
|
|
|
|
|
476 C.E.
|
|
Traditional “fall” of Rome
|
|
524 C.E.
|
|
Death of BoethiusAnicius
Manlius Severinus Boethius (480 – 524 C.E.)
Boethius is considered to be one of the foremost scholars of the Dark
Ages. Education and knowledge were important to Boethius and he is
credited with writing the material for the quadrivium, an educational
course (originally taught in monasteries) consisting of four topics:
arithmetic, geometry, astronomy, and the theory of music. Although his
mathematical background was very limited his fluency in Greek allowed
him to translate portions of Euclid's Elements and write a book on
arithmetic. These books were of poor quality but they were all that
were available at the time.
|
|
|
|
|
529 C.E.
|
|
Closing of the schools
at AthensThe Platonic Academy at Athens had been in existence for
over 900 years. During the time of Proclus (410 C.E. - 485 C.E.) it had
become the center of Neoplatonic learning. When Justinian became
emperor in the East (the Byzantine Empire), in 527 C.E., he felt the
schools' teachings were a threat to orthodox Christianity and in 529
had the schools closed and the scholars dispersed.
|
|
|
|
|
530 C.E.
|
|
Eutocius' commentaries
on ArchimedesEutocius of Ascalon (ca. 480 C.E. - 540 C.E.)
Eutocius wrote commentaries on three works of Archimedes. It is
believed that the first of Eutocius's commentaries on Archimedes was
written around 510. His most famous is probably his commentary on
Archimedes' On the Sphere and Cylinder.
Eutocius also edited and wrote commentaries on the first four books of
the Conics of Apollonius.
|
|
|
|
|
641 C.E.
|
|
Library at Alexandria
burnedAt its peak, the Library of Alexandria was reported to
contain over 500,000 volumes. These volumes were collected in an
unusual way. By a decree of Ptolemy III, all visitors to the city were
required to surrender all books and scrolls in their possession; these
writings were then copied by royal scribes. The originals were kept and
put into the Library, and the copies were then given to the previous
owners.
The Library of Alexandria is surrounded by a variety of contradictions
concerning its destruction. When Julius Caesar torched the fleet of
Cleopatra's brother and rival monarch during his invasion of Alexandria
in 47–48 B.C.E. some claim that the resulting fire destroyed the
Library; however, it is more often reported that a warehouse near the
fleet which contained about 40,000 volumes was burned. Several other
destructions have been reported with the final one being a burning in
641 C.E.
supposedly at the hands of Muslim invaders. Since the Library most
likely consisted of more than one building, it is possible that when
any one of the buildings was destroyed it could have been called the
destruction of the Library.
|
|
|
|
|
|
|
|
732 C.E.
|
|
Battle of ToursThe
Battle of Tours: 732
After the conquest of Syria, Egypt, and North Africa, a Moslem army
began to invade Western Europe with the goal of crushing Christianity.
Abd-er Rahman led an army numbering between 60,000 and 400,000 soldiers
across the Western Pyrenees. They were met outside of Tours by the
Frankish Army led by Charles Martel. Even though the Moslem army had a
vast cavalry and the Frankish Army was on foot, the terrain did not
favor the horsemen and foot soldiers prevailed.
October 10, 732 C.E. marks the conclusion of the Battle of Tours. The
battle ended with the death of Abd-er Rahman. Martel expected the
Moslems to regroup and attack but they merely withdrew with the loss of
their leader. This was probably one of the most decisive battles in all
of history.
|
|
775 C.E.
|
|
Hindu works translated
into ArabicMuslims have made immense contributions to almost all
branches of the sciences, but mathematics appeared to be their favorite
subject. Although much original mathematics is attributed to the Arabs,
they obtained much by “inheritance.” The mathematical knowledge Arabs
inherited came from two basic sources--the Hindus and the Greeks. The
Greek works came mostly from Alexandria and the Hindu works were
translated during the 8th Century C.E.
|
|
|
|
|
|
|
|
814 C.E.
|
|
Death of CharlemagneCharlemagne
(c. 747 – 814)
Considered the founder of the Frankish Empire in Western Europe,
Charlemagne was the elder son of Pepin the Short. Charlemagne was
engaged in almost constant battle throughout his reign. He proceeded to
force Catholicism on the conquered, and those who refused to convert
were slaughtered.
On a more positive note, Charlemagne took a serious effort in his and
others' scholarship and had learned to read in his adulthood. This was
quite an achievement for kings at this time, since most were
illiterate. He gave Alcuin of York (c 735-804) the task of establishing
schools throughout his realm. He also made an effort to establish
formal culture. His palace school at Aachen was a center of studies and
the arts.
|
|
830 C.E.
|
|
Al-Khowarizmi's Algebra
Algebra was one of the major Arabic contributions to
mathematics. It is from the Arabs that we get the name “algebra” it
came from the title of a text book in the subject, Hisab al-jabr w'al
muqabala, written about 830 C.E. by the astronomer and mathematician
Mohammed ibn-Musa al-Khowarizmi. In addition our word "algorithm" in a
corruption of al-Khowarizmi's name. Al-Khowarizmi's book became the
standard for algebra and was used in Europe in the 13th Century.
|
|
|
|
|
|
|
|
999 C.E.
|
|
Gebert becomes Pope Sylvester II
|
|
|
|
|
1066 C.E.
|
|
Battle of Hastings The
Battle of Hastings in 1066 was the last time England was successfully
invaded and conquered by a foreign army.
|
|
|
|
|
1096 C.E.
|
|
First Crusade
|
|
1114 C.E.
|
|
Birth of BhaskaraBhaskara
(1114 – 1185) Indian
Bhaskara is also known as Bhaskara II or as Bhaskaracharya (meaning
"Bhaskara the Teacher"). Bhaskara is considered to represent the peak
of mathematical knowledge in the 12th century. He attained an
understanding of the number systems and solving equations which was not
to be achieved in Europe for several more centuries.
An animation of Bhaskara's dissection proof of the Pythagorean Theorem
can be found at
http://www.math.wichita.edu/~richardson/
under “Things of Interest”, Pythagorean Theorem
|
|
|
|
|
1142 C.E.
|
|
Adelard of Bath
translated EuclidAdelard of Bath (c.1080-c.1160)
Adelard has been called the first English scientist. He wrote papers on
the abacus and on the astrolabe, the most important scientific
instrument of his time. In addition to translating Euclid, he
translated Arabic works in mathematics and astronomy (with
commentaries). These translations helped introduce Hindi-Arabic
numerals and the use of zero to the west. In his book on Natural
Philosophy he showed how reason and observation could be used to
explain natural phenomena.
|
|
|
|
|
|
|
|
1170 C.E.
|
|
Murder of Thomas
à BecketThomas Becket (1118 – 1170)
The life of Thomas Becket, Archbishop of Canterbury, ended with a blow
from a sword on a December evening in 1170. Historians have laid the
blame for the murder of Becket on his former close personal friend,
King Henry II. King Henry II had appointed Becket to the top post of
the Church believing that he was appointing someone he could control.
However, Becket's allegiance shifted from the court to the Church.
|
|
1202 C.E.
|
|
Fibonacci's Liber
abaciLeonardo Pisano Fibonacci (1170 – 1250 C.E.)
Fibonacci was born in Italy but was educated in North Africa. He
traveled to North Africa with his father, who was a diplomat
representing merchants of the Republic of Pisa. Fibonacci was taught
mathematics by Arab tutors and from their teachings recognized the
enormous advantages of the Hindu-Arabic number system and the
mathematical systems developed from this number system.
Fibonacci ended his travels around the year 1200 and returned to Pisa.
He then wrote a number of important texts. Of his books four have
survived: Liber abaci, Practica geometriae, Flos,
and Liber quadratorum. Since books in this time period were
hand written and copied by hand, we are fortunate to have access to his
writing in these works.
In Liber abaci the famous rabbit problem is found which lead
to the sequence now referred to as the Fibonacci Sequence. The main
thrust of Liber abaci was introduce Arabic arithmetic and
algebra to Europe.
|
|
|
|
|
|
|
|
1204 C.E.
|
|
Crusaders sack Constantinople
|
|
|
|
|
1215 C.E.
|
|
Magna Carta
|
|
1270 C.E.
|
|
William of Moerbeke
translated ArchimedesWilliam of Moerbeke (ca. 1215 – 1286)
William of Moerbeke was a 13th Century scholar who was the most
prolific medieval translator of philosophical, medical, and scientific
texts from Greek into Latin. The Vatican collection holds William's own
copy of the translation he made of Archimedes' work. It is through
William of Moerbeke's translations that we still have copies of
Archimedes works, for many of Archimedes actual works have since been
lost.
|
|
|
|
|
|
|
|
1271 C.E.
|
|
Travels of Marco Polo:
mechanical clocks (approx.)
|
|
|
|
|
1286 C.E.
|
|
Invention of eyeglasses (approx.)
|
|
1303 C.E.
|
|
Chu Shih-Chieh and the
Pascal triangle (long before Pascal)Chu Shih-Chieh (also known as
Zhu Shijie) (ca.1260 – ca. 1320 C.E.)
Disclaimer: Please excuse my ignorance of the nuances of the Chinese
language. I find different spellings and, to me, totally different
names for people and titles of books.
The text Siyuan yujian published in 1303 contains a diagram, in Chinese
symbols, of Pascal's triangle giving the binomial coefficients up to
the eighth powers. This is reported to be a copy of a more ancient
work. Thus the triangle we refer to as Pascal's triangle was known long
before Pascal's time.
|
|
|
|
|
|
|
|
1348 C.E.
|
|
The Black DeathThe
Black Death, 1348
The Black Death spread from the East and reached the shores of Italy in
the spring of 1348. It unleashed a three-year rampage of death across
Europe unprecedented in recorded history. In this period, anywhere from
25% to 50% of Europe's population had fallen victim.
The plague presented itself in three interrelated forms: the bubonic
variant (the most common derives its name from the swellings or buboes
that appeared on a victim's neck, armpits or groin); pneumonic plague
(which attacked the respiratory system and was spread by merely
breathing the exhaled air of a victim); and the septicemic version of
the disease (which attacked the blood system.)
|
|
|
|
|
1364 C.E.
|
|
Death of Petrarch
|
|
|
|
|
1431 C.E.
|
|
Joan of Arc burned
|
|
|
|
|
1440 C.E.
|
|
Invention of the
printing pressThe invention of the printing press in 1440 C.E.
was a major step forward in literacy. Prior to Johannes Gutenberg's
solution to the problem of molding movable type, books were hand
written and hand copied. Thus, only the very wealthy could afford to
have copies of books made. The development of printing presses that
could produce hundreds of books in a short period of time stimulated
intellectual life. Before long it was no longer the exclusive domain of
the churches and courts. The printing press helped usher in an era of
enlightenment.
|
|
|
|
|
1453 C.E.
|
|
Fall of Constantinople
|
|
1464 C.E.
|
|
Death of Nicolas of CusaNicholas
of Cusa (1401 – 1464) Germany
Nicholas of Cusa wore many hats: Papal Vicar, Papal Legate, Cardinal,
Prince-bishop, Diplomat, Lawyer, Mathematician, Astronomer, Humanist,
Theologian, Philosopher, and Historian.
Giordano Bruno is said to have written:
If [Nicholas of Cusa] had not been hindered by his priest's vestment,
he would have even been greater than Pythagoras!
His main interests in mathematics were in geometry and logic. This
included studying the infinitely large and the infinitely small.
His interest in astronomy led him to theories which are true (and
others which may still prove to be true). Unique for his time, he
claimed the following: that the Earth moved round the Sun; that the
stars were other suns; and that space was infinite. (He also believed
that the stars had other worlds orbiting them which were inhabited.)
These were rather radical theories for a priest!
|
|
|
|
|
1482 C.E.
|
|
First printed edition of
Euclid's ElementsErhard Ratdolt (1447 – 1527) German
Ratdolt produced the first printed edition of Euclid's Elements.
It was a Latin translation by Johannes Campanus. This is acknowledged
to be the first mathematical book of significance to appear in print.
Prior to this, all mathematical books were hand written. This was also
the first printed book illustrated with geometric figures.
|
|
|
|
|
|
|
|
1483 C.E.
|
|
Murder of the princes in the Tower
|
|
|
|
|
1485 C.E.
|
|
Henry VII, the first Tutor
|
|
1489 C.E.
|
|
Use of + and – by WidmannJohannes
Widman (1462 – 1498)
Widman is best known for an arithmetic book he wrote in 1489 (in
German) which contains the first recorded appearance of + and - signs.
This book was better than those that came before it in that it had
more, and a wider range, of examples. His book was reprinted until
1526. At this time Adam Ries and others wrote superior books.
|
|
|
|
|
1492 C.E.
|
|
Use of decimal point by
PellosFrancesco Pellos (fl. 1450 – 1500)
In the year Columbus discovered America, Francesco Pellos wrote a
commercial arithmetic book, Compendio de lo abaco, in which he made use
of a dot to denote the division of an integer by a power of ten. This
lead to the development of what we now refer to as a decimal point.
|
1492 C.E.
|
|
Columbus discovers the Americas
|
|
|
|
|
1517 C.E.
|
|
Protestant Reformation
|
|
|
|
|
1520 C.E.
|
|
Field of the Cloth of Gold
|
|
1527 C.E.
|
|
Apian publishes the
Pascal trianglePeter Apian (1495 – 1552) Germany
In 1527 Peter Apian published an arithmetic book in which the title
page contained a copy of a Pascal Triangle. This is the first printed
version of Pascal's Triangle and it appeared more than a century before
Pascal's investigation of the properties of this triangle.
|
|
|
|
|
|
|
|
1534 C.E.
|
|
Act of SupremacyThe
Act of Supremacy was English legislation that was passed in 1534. It
declared that the sovereign (King of England) is Supreme Head of the
Church of England.
|
|
1543 C.E.
|
|
Tartaglia publishes
Moerbeke's translation of
ArchimedesNicolo Tartaglia (1499 – 1557) Italian
Some think that Tartaglia was cheated when Cardan, after taking an oath
not to do so, published Tartaglia's method of solving a cubic in his Ars
magna. However, Tartaglia was not above passing other's work off
as his own. In 1543 he published material derived from Moerbeke's
translation of Archimedes as if it were his own work.
|
|
|
|
|
1544 C.E.
|
|
Stifel publishes Arithmetica
integraMichael Stifel (1487 – 1567) Germany
Stifel's research emphasized arithmetic and algebra. He is credited
with inventing logarithms independently of Napier using a totally
different approach. In 1544 he published his most famous work, Arithmetica
integra. This work contains binomial coefficients and the notation
+, - .
Stifel also dabbled in numerology. He tried to predict the end of the
world and in a most creative way assigned the number of the beast (666)
to Pope Leo X.
|
|
|
|
|
1545 C.E.
|
|
Cardan publishes Ars
magnaGirolamo Cardano (A.K.A. Cardan) (1501 – 1576) Italian
Cardan was a man of many talents of which mathematics was one. He is
best remembered for his work on solving cubic and quartic equations.
Some of his work on cubic equations was obtained from Tartaglia. He
took an oath that he would not publish Tartaglia's method until after
Tartaglia had published. However, Cardan broke this promise when, in
1545, he published his greatest mathematical work Ars Magna.
In it he gave the methods of solution of the cubic and quartic
equation. In 1543 he discovered that Tartaglia was not the first to
solve the cubic equation by radicals and as a result felt that he could
publish what Tartaglia had given him despite his oath.
|
|
|
|
|
|
|
|
1553 C.E.
|
|
Servetus burned at GenevaMichael
Servetus (ca. 1509 – 1553)
Michael Servetus was a Spaniard martyred in the Reformation for his
criticism of the doctrine of the trinity and his opposition to infant
baptism. He has the distinction of being burned at the stake by the
Protestants and then a few months later he was again executed, this
time in effigy, by the Catholic Inquisition in France.
|
|
|
|
|
1558 C.E.
|
|
Accession of Elizabeth I in England
|
|
1564 C.E.
|
|
Birth of Galileo
|
1564 C.E.
|
|
Birth of Shakespeare and death of Michelangelo
|
|
1572 C.E.
|
|
Bombelli's AlgebraRafael
Bombelli (1526 – 1572) Italy
Contrary to what many people believe, complex arithmetic did not arise
from the solution of quadratic equations. The need really arose from
the use of the Cardan-Tartaglia formula for the solution of a cubic
equation. For example, the equation x3 = 15x + 4 has an
obvious positive solution, x = 4. However, when the Cardan-Tartaglia
formula is applied one gets expressions involving the square root of –
121. Bombelli is responsible for resolving this conflict by introducing
the arithmetic of complex numbers. This he introduces in his work,
Algebra, which gave a thorough treatment of the algebra then known as
well as his important treatment of complex numbers.
|
1572 C.E.
|
|
Saint Bartholomew's Day
Massacre
(French
religious war)August 24, 1572, was the date of the infamous St.
Bartholomew's Day Massacre in France. At this time more than a third of
the French population had adopted the Protestant faith. This raised an
alarm in the Vatican. The Catholic Church was fearful of losing its
power in France. The King's spiritual adviser, a Jesuit priest, urged
the King to massacre the Protestants. The massacre began in Paris and
spread rapidly. It is hotly debated as to whether the Pope encouraged
the attack on Protestant leaders; however, the Vatican was pleased with
the results and a mural depicting the Massacre was commissioned by the
Pope.
|
|
1579 C.E.
|
|
Viète publishes Canon
mathematicusFrançois Viète (1540 – 1603) French
Although he was not a professional mathematician, his work deciphering
cryptic messages of the enemy as a member of the king's council for
Kings Henry III and IV fueled his interest in mathematics. He made
significant contributions to arithmetic, algebra, trigonometry and
geometry. He was a strong proponent of the decimal system and in his
book Canon Mathematicus he made the case for using decimal
fractions
rather than sexagesimal fractions. (It should be noted that until this
time the Babylonia system of fractions was commonly used.)
|
|
|
|
|
|
|
|
1584 C.E.
|
|
Assassination of William of Orange
|
|
|
|
|
1588 C.E.
|
|
Drake's defeat of the Spanish armada
|
|
1595 C.E.
|
|
Pitiscus publishes TrigonometriaBartholomeo
Pitiscus (1561 – 1613) Polish/German
Pitiscus is credited with coining the word “trigonometry” which
appeared in the title of his 1595 book, Trigonometria. This
work consisted of five books on plane and spherical trigonometry. After
his death the work was translated into English in 1614 and French in
1619.
|
|
|
|
|
|
|
|
1598 C.E.
|
|
Edict of NantesThe
Edict of Nantes of 1598 implemented the belief that the government
should not prescribe religious belief and conduct. Until the Edict of
Nantes, for most of the second half of the 16th Century, France was
embroiled in wars of religion. (See for example, Saint Bartholomew's
Day Massacre.) The two main adversaries were the Calvinist protestants
and the Catholics. Both sides felt that in order to have a strong
kingdom only one religion could be permitted to exist.
|
|
|
|
|
1603 C.E.
|
|
Death of Elizabeth I
|
|
1609 C.E.
|
|
Kepler's Astronomia
novaJohann Kepler (1571 – 1630) Germany
Kepler considered himself to be a mathematician who studied astronomy.
With the help of the enormous number of observations made by Tyco
Brahe, Kepler established the laws of planetary motion. In Astyronomia
nova he gave his first two laws of astronomy: (1) The planets move
about the Sun in elliptical orbits with the Sun at one focus. (2) The
radius vector joining a planet to the Sun sweeps out equal areas in
equal time.
In computing the areas in the second law, Kepler thought of the areas
as being formed by a collection of infinitely small triangles with one
vertex at the Sun and the other two on the orbit. He then used a form
of what we would now call integral calculus to compute the areas.
:
Galileo's
telescope
|
|
|
|
|
1614 C.E.
|
|
Napier's logarithmsJohn
Napier (1550 – 1617) Scotland
It appears that Napier's study of mathematics was only a hobby for him
and that he often found it hard to find the time for the necessary
calculations between working on theology. We know him best for his
invention of logarithms but he also developed an invention called
"Napier's bones" used for mechanically multiplying dividing and taking
square roots and cube roots.
Logarithms we use today are specified to be of a certain base; however,
Napier's logarithms are not really to any base although in our present
terminology we might say that they are to base 1/e. It was Henry Briggs
(1561-1630), an Englishman, who improved on Napier's work and was most
responsible for the acceptance of logarithms by scientists.
|
|
|
|
|
|
|
|
1616 C.E.
|
|
Deaths of Shakespeare and Cervantes
|
|
1620 C.E.
|
|
Bürgi's logarithmsJobst
Bürgi (1552 – 1632) Switzerland
Jobst Bürgi developed the idea of logarithms independently of
Napier. Even though he started his investigation in 1588, about 6 years
before Napier, he did not publish his results until 1620, about twelve
years after Napier published his results. As a result Napier is
credited with the development of logarithms and very few know the name
Bürgi. If Bürgi had published before Napier, Napier would be
the forgotten one since Bürgi's logarithms are very close to our
natural logarithms.
|
1620 C.E.
|
|
Landing of Pilgrims in America
|
|
|
|
|
1626 C.E.
|
|
Death of Francis Bacon
|
|
|
|
|
1628 C.E.
|
|
Harvey's De motu cordis et sanguinis
|
|
1629 C.E.
|
|
Fermat's method of
maxima and minimaPierre de Fermat (1601 – 1665) French
We know Fermat best for his work in number theory and, of course, his
famous theorem that Wiles proved in 1994. However, Fermat, even though
he was not a professional mathematician, made significant contributions
to the field. In 1629, while in Bordeaux, he produced important work on
maxima and minima problems. His method of finding extrema was much like
our current methods; however, his system of mathematical symbols made
his work very awkward. He was using the system of mathematical symbols
devised by François Viète.
|
|
|
|
|
|
|
|
1636 C.E.
|
|
Harvard College founded
|
|
1637 C.E.
|
|
Descartes' Discours
de la méthodeRené Descartes (1596 – 1650)
French
René Descartes was a philosopher whose treatise on science under
the title Discours de la méthode pour bien conduire sa raison et
chercher la vérité dans les sciences contained an
appendix titled La Géométrie which presents his
application of algebra to geometry. This became one of the most
important contributions to mathematics. For the resulting Cartesian
geometry made the study of mathematics more accessible to people less
skilled in formal geometry.
|
|
|
|
|
1639 C.E.
|
|
Desargues' Brouillon
project Girard Desargues (1591 – 1661) French
Desargues invented a new form of geometry, projective geometry, and it
was presented in a 1639 essay to be called Brouillon project d'une
atteinte aux evenemens des rencontres du Cone avec un Plan;
however, it appeared under the title Rough Draft. The end result of his
work was a unified theory of conics. His work might have had a more
immediate impact if it had not appeared just two years after Descartes'
monumental work in geometry.
|
|
|
|
|
1640 C.E.
|
|
Pascal's Essay pour
les coniquesBlaise Pascal (1623 – 1662) French
Blaise Pascal had his first work, Essay pour les coniques
(Essay on Conic Sections) published in February 1640 at the ripe old
age of 17! Pascal's father Étienne Pascal did not want Blaise to
study mathematics until he was 15, but at the age of 12 he discovered
that
the sum of the angles of a triangle are two right angles and, when his
father found out, he relented and gave Blaise a copy of Euclid. Blaise
Pascal was one of the great French mathematicians of the 17th, or any,
Century.
|
|
|
|
|
1642 C.E.
|
|
Birth of Newton: Death
of GalileoGalileo Galilei (1564 – 1642) Italian
Sir Isaac Newton (1642 – 1727) English
Some find it coincidental that Newton was born the year that Galileo
died. These two men had a great impact on our understanding of the
universe. However, using the “corrected" Gregorian calendar date,
Newton was born on January 4, 1643 rather than Christmas Day, 1642. The
discrepancy occurs since England did not adopt the Gregorian calendar
until 1752. It should be noted that the Julian calendar was switched
over to the Gregorian starting in 1582, but not everyone accepted the
new calendar immediately.
|
|
|
|
|
|
|
|
1643 C.E.
|
|
Assassination of Louis XIV
|
|
|
|
|
1644 C.E.
|
|
Torricelli's Barometer
|
|
|
|
|
1649 C.E.
|
|
Charles I beheaded
|
|
1655 C.E.
|
|
Wallis publishes Arithmetica infinitorium
|
|
|
|
|
1658 C.E.
|
|
Huygens' cyclodial pendulum clock
|
|
|
|
|
|
|
|
1660 C.E.
|
|
The Restoration
|
|
1662 C.E.
|
|
Royal Society founded
|
|
|
|
|
1666 C.E.
|
|
Académie des Sciences founded
|
|
|
|
|
1667 C.E.
|
|
Gregory's Geometriae
pars universalisJames Gregory (1638 – 1675) Scotland
In 1667 Gregory published Geometriae pars universalis which
in reality was probably the first attempt at writing a text-book on the
calculus. Gregory was a brilliant mathematician but one who was
reluctant to publish his findings. His discoveries predate many of
those of Newton, Taylor and Cauchy - to name just a few.
|
|
|
|
|
1668 C.E.
|
|
Mercator publishes Logarithmotechnia
|
|
|
|
|
1670 C.E.
|
|
Barrow's Lectiones geometriae
|
|
|
|
|
1678 C.E.
|
|
Ceva's TheoremGiovanni
Ceva (1648 – 1734) Italy
In a time when most mathematicians were concerned with analytic
geometry and calculus, the Italian mathematicians were still focusing
on Euclidean geometry. The most notable contribution to Euclidean
geometry during this time was Ceva's Theorem which states: A necessary
and sufficient condition that lines from the vertices A, B, C of a
triangle to points D, E, F on the opposite sides be concurrent is that
(BD/DC)(CE/EA)(AF/FB)=1.
Ceva's Theorem greatly simplified some of the proofs of major theorems
in Euclidean geometry. This theorem is closely related to Menelaus'
Theorem which was lost for centuries but rediscovered by Ceva and
published with his theorem in 1678.
|
|
|
|
|
|
|
|
1679 C.E.
|
|
Writ of Habeas CorpusHabeas
corpus in England
The procedure for the issuing of writs of habeas corpus was first
codified by the Habeas Corpus Act 1679, following judicial rulings
which had restricted the effectiveness of the writ. Since the 18th
century the writ of habeas corpus has been used in cases of unlawful
detention by private individuals. The writ of habeas corpus serves as
an important check on the manner in which courts pay respect to lawful
rights.
Prisoners often seek release by filing a petition for a writ of habeas
corpus. A writ of habeas corpus is a judicial mandate to a prison
official ordering that an inmate be brought to the court so it can be
determined whether or not that person is imprisoned lawfully and
whether or not he should be released from custody.
|
|
|
|
|
1683 C.E.
|
|
Siege of Vienna
|
|
1684 C.E.
|
|
Leibniz' first paper on
the calculus Gottfried Wilhelm von Leibniz (1646 – 1716)
In 1684 Leibniz published details of his differential calculus in Acta
Eruditorum, a journal established in Leipzig two years earlier.
The
paper contained the rules for computing the derivatives of powers,
products and quotients using the now the familiar d notation.
The paper contained no proofs and was criticized for this by Jacob
Bernoulli.
|
|
|
|
|
|
|
|
1685 C.E.
|
|
Revocation of the Edict of Nantes
|
|
1687 C.E.
|
|
Newton's PrincipiaIsaac
Newton (1642-1727)
The actual, full title of this work is Philosophiae Naturalis
Principia Mathematica or The Mathematical Principles of
Natural Philosophy. It is commonly known simply as the Principia
and
it is considered to be one of the most important single works in the
history of modern science. This work contains Newton's version of the
calculus. Even though he began his development of the calculus before
Leibniz, Newton was reluctant to publish and as a result a great
controversy arose as to who should get the credit. It should be noted
that the Principia contained much more than just Newton's
calculus.
|
|
|
|
|
|
|
|
1689 C.E.
|
|
The Glorious Revolution
|
|
1690 C.E.
|
|
Rolle's Trait d`algèbre
|
|
|
|
|
1696 C.E.
|
|
The Bernoulli's Brachistochrone and L'Hospital's
Rule
|
|
|
|
|
|
|
|
1702 C.E.
|
|
The start of Queen Anne's War
|
|
1706 C.E.
|
|
The use of the symbol π
by William JonesWilliam Jones (1675 – 1749) Welsh/English
In 1706 William Jones published his New Introduction to Mathematics
in which he introduced the symbol π. It appears he used the symbol
repeatedly to denote the (periphery) circumference of a circle with
unit diameter – which is π.
|
|
|
|
|
1715 C.E.
|
|
Taylor's Methodus incrementorium
|
|
|
|
|
1718 C.E.
|
|
De Moive's Doctrine of Chances
|
1718 C.E.
|
|
Fahrenheit's thermometer
|
|
1730 C.E.
|
|
Stirling's formula
|
|
|
|
|
1733 C.E.
|
|
Saccheri's attempt to
vindicate EuclidGirolamo Saccheri (1667-1733)
Saccheri made the first serious study of the logical consequence of an
actual denial of the fifth postulate. His aim was to assume the
postulate false and then derive it as a logical consequence. Saccheri
began by considering a quadrilateral ABCD with sides AD and BC equal
and perpendicular to the base AB. Saccheri then demonstrated that the
summit angles at C and D were equal. From this he then declared three
hypotheses: (1) angle C = angle D > 90° (obtuse case); (2) angle
C = angle D <90°(acute case); and (3) angle C = angle D =
90° (right angle case). He then proceeded to prove that if one of
these hypotheses were true for one of his quadrilaterals, then it would
be true for every such quadrilateral. He then showed that if the obtuse
case held then the sum of the angles of a triangle would be greater
than two right angles. He had little difficulty in convincing himself
that this was impossible. He next attacked the acute case. Here he had
great difficulty in convincing himself of the fact that this case was
impossible. In fact, he came very close to discovering the first
non-Euclidean geometry; however, his faith in Euclid was so strong that
he denied this possibility. He eventually declared that the acute
hypothesis was false leaving only the right angle hypothesis which was
equivalent to the fifth postulate. Saccheri's goal was to vindicate
Euclid.
|
|
|
|
|
1734 C.E.
|
|
Berkeley's The Analyst
|
|
|
|
|
|
|
|
1740 C.E.
|
|
Accession of Frederick the Great
|
|
1742 C.E.
|
|
Maclaurin's Treatise of Fluxions
|
1742 C.E.
|
|
Centigrade thermometer
|
|
1748 C.E.
|
|
Euler's Introductio
in analysin infinitorumLeonhard Euler (1707 – 1783) Swiss
Leonhard Euler was probably the most prolific publisher of mathematics
of all time. His research covered most all areas of mathematics known
at his time. Students of mathematics today find his name in almost all
courses they take. It is claimed that mathematical analysis began with
Euler. In 1748 he published Introductio in analysin infinitorum
in which he gave a more precise definition of function and made
mathematical analysis the study of functions. In this work he bases the
calculus on the theory of elementary functions rather than on geometric
curves, as had been done previously. :
Agnesi's Istituzioni
AnaliticheMaria Gaëtana Agnesi (1718 – 1799) Italian
Maria Gaëtana Agnesi showed remarkable talents very early in life
and since her father could afford to give her high quality tutors she
mastered many languages such as Latin, Greek and Hebrew at an early
age. Much of her mathematics she studied on her own. She became very
familiar with the works of Newton and L'Hospital. Out of this
understanding came her famous book Instituzioni Analitiche, a
book on differential calculus. She wrote the book in Italian as a
teaching text and it was a significant book for studying the calculus
for many years.
|
|
|
|
|
1750 C.E.
|
|
Cramer's Rule
|
|
|
|
|
|
|
|
1752 C.E.
|
|
Franklin's kite experiment
|
|
|
|
|
1767 C.E.
|
|
Watt's improved steam engine
|
|
1770 C.E.
|
|
Hyperbolic trigonometry
|
|
|
|
|
|
|
|
1774 C.E.
|
|
Discovery of oxygen
|
|
|
|
|
1776 C.E.
|
|
American Declaration of
IndependenceThe Declaration of Independence of the Thirteen
Colonies
The Declaration of Independence could be considered a mathematical
document. Thomas Jefferson was a well educated man who believed that
all educated people should know mathematics at least through
trigonometry. He was impressed by the formal nature of mathematics and
it appears this carried over into the writing of the Declaration of
Independence. In the second paragraph he proposes his axioms (“We hold
these truths to be self-evident, ...”). He then states his theorem that
the Colonies should withdraw from the rule of King George III. He then
supplies the proof for his theorem. “To prove this, let Facts be
submitted to a candid world. ... “
|
|
1777 C.E.
|
|
Buffon's needle problemGeorges
Louis Leclerc Comte de Buffon (1707 – 1788) French
Buffon was a well-educated man who wrote on a wide range of topics that
included mathematics, the theory of probability, astronomy and physics,
especially optics. His most referenced contribution to mathematics was
a geometrical probability experiment. He threw sticks over his shoulder
onto a tiled floor and counted the number of times the sticks fell
across the lines between the tiles. His conclusion was that the the
number of successes was related to the area under a cycloid whose
generating circle has a diameter equal to the length of the stick.
The current problem, known as the "Buffon Needle Problem", is to drop a
needle on a lined sheet of paper and determine the probability of the
needle crossing one of the lines on the paper.
|
|
|
|
|
1781 C.E.
|
|
Discovery of Uranus by Herschel
|
|
|
|
|
1788 C.E.
|
|
Lagrange's Mécanique analytique
|
|
|
|
|
|
|
|
1789 C.E.
|
|
French Revolution
|
|
1794 C.E.
|
|
Legendre's Elements de
géométrie
|
1794 C.E.
|
|
Lavoisier (father of
modern chemistry) guillotined Antoine Lavoisier (1743 – 1794)
French
Lavoisier originally studied law at the urgings of his family; however
at age 21 he began to fulfill his dream to study mathematics and
science. He studied astronomy, botany and geology under eminent
scientists of the time. From 1770 to 1790 the science of chemistry was
radically changed and Lavoisier was the principle mover and hence has
been referred to as the Father of Modern Chemistry.
In 1768 he joined a tax collecting agency that collected taxes for the
Crown. He worked for this firm in order to earn money to continue his
work in chemistry. Although he discharged his duties honestly, the
revolution zealots found him guilty of conspiracy against the people of
France and sentenced him to die. He was guillotined on May 8, 1794.
|
|
|
|
|
1795 C.E.
|
|
École Polytechnique and
École Normale established
|
|
1796 C.E.
|
|
Laplace's Systeme du monde (nebular
hypothesis )
|
1796 C.E.
|
|
Vaccination
|
|
1797 C.E.
|
|
Lagrange's Fonctions analytique
|
|
|
|
|
|
|
|
1799 C.E.
|
|
Metric system introduced
|
|
|
|
|
1800 C.E.
|
|
Volta's battery
|
|
1801 C.E.
|
|
Gauss' Disquisitiones arthmeticae :
Ceres discovered
|
|
|
|
|
|
|
|
1803 C.E.
|
|
Dalton's atomic theory
|
|
|
|
|
1804 C.E.
|
|
Napoleon crowned emperor
|
|
1810 C.E.
|
|
Gergonne started the journal Annales
|
|
|
|
|
|
|
|
1815 C.E.
|
|
Battle of Waterloo
|
|
|
|
1820 C.E. |
|
Oersted discovered
electromagnetism |
| 1822
C.E. |
|
Fourier series |
|
|
|
| 1826
C.E. |
|
Crelle's Journal founded:
Principle of Duality:
Elliptic functions |
1826 C.E. |
|
Ampere's work in
electrodynamics |
| 1827
C.E. |
|
Cauchy's Calculus
of Residues |
1827 C.E. |
|
Ohm's Law |
| 1829
C.E. |
|
Lobachevskian geometry:
Death of Abel |
|
|
|
|
|
|
1831 C.E. |
|
Faraday's
electromagnetic induction |
| 1832
C.E. |
|
Death of Galois:
Babbage's Analytical Engine |
|
|
|
| 1836
C.E. |
|
Liouville's Journal founded |
1836 C.E. |
|
Telegraph invented |
| 1843
C.E. |
|
Hamilton's quaternions |
|
|
|
|
|
|
1846 C.E. |
|
Neptune discovered:
Use of anesthesia |
|
|
|
1848 C.E. |
|
Marx's Communist
Manifesto |
|
|
|
1850 C.E. |
|
Dickens' David
Copperfield |
| 1854
C.E. |
|
Boole' Laws of
Thought |
|
|
|
|
|
|
1858 C.E. |
|
The Atlantic cable
laid |
|
|
|
1859 C.E. |
|
Darwin's Origin of
Species |
|
|
|
1861 C.E. |
|
Start of American
Civil War |
|
|
|
1865 C.E. |
|
Assassination of
Abraham Lincoln |
|
|
|
1868 C.E. |
|
Cro-Magnon caves
discovered |
|
|
|
1869 C.E. |
|
Suez Canal finished |
| 1873
C.E. |
|
Hermite proved e
transcendental |
|
|
|
| 1874
C.E. |
|
Cantor's Mengenlehre |
|
|
|
|
|
|
1876 C.E. |
|
Alexander Bell's
telephone |
| 1882
C.E. |
|
Lindemann proved π transcendental |
|
|
|
| 1888
C.E. |
|
American Mathematical Society founded |
1888 C.E. |
|
Pasteur Institute
founded |
| 1889
C.E. |
|
Peano's postulates |
|
|
|
|
|
|
1895 C.E. |
|
Roentgen discovered
X-rays |
| 1896
C.E. |
|
Prime Number Theorem proved |
1896 C.E. |
|
Discovery of
radioactivity |
|
|
|
1897 C.E. |
|
Electrons discovered |
|
|
|
1898 C.E. |
|
Radium dscovered |
| 1899
C.E. |
|
Hilbert'sGrundlagen
der GeometrieDavid Hilbert (1862 – 1943) Born in Prussia,
died in Germany
Hilbert was one of the great mathematicians of the 19th and 20th
Centuries. No person has had a greater influence on geometry since
Euclid. In 1899 Hilbert, after a systematic study of the axioms of
Euclidean geometry, proposed his own collection of 21 such axioms and
he analyzed their significance. He then published Grundlagen der
Geometrie which solidly put geometry in a formal axiomatic
setting. The book was a major influence in promoting the axiomatic
approach to mathematics which has been one of the major characteristics
of the subject throughout the 20th century. |
|
|
|
| 1900
C.E. |
|
Hilbert's ProblemsDavid
Hilbert (1862 – 1943) Born in Prussia, died in Germany
Hilbert was one of the great mathematicians of the 19th and 20th
Centuries. He was challenged to determine the route of mathematical
research in the 20th Century and at the Second International Congress
of Mathematicians in Paris Hilbert delivered his famous speech “The
Problems of Mathematics” which left mathematicians with 23 challenging
problems. Some, but not all, of these problems have been solved to date.
In 1930 Hilbert gave an address (at his retirement) which ended with
six famous words which showed his enthusiasm for mathematics and his
life devoted to solving mathematical problems. “Wir müssen wissen,
wir werden wissen” We must know, we shall know. :
Russell and
Whitehead's Principia, Vol.1 |
1900 C.E. |
|
Freud's Die
Traumdeutung |
| 1901
C.E. |
|
Planck's quantum theory |
1901 C.E. |
|
First radio receiver |
| 1903
C.E. |
|
Lebesgue integration |
1903 C.E. |
|
First powered air
flight |
| 1905
C.E. |
|
Einsteins's special relativity |
|
|
|
|
|
|
1906 C.E. |
|
Kellogg invents
cornflakes |
|
|
|
1908 C.E. |
|
Model T Ford |
|
|
|
1914 C.E. |
|
Assassination of
Austrian Archduke Francis Ferdinand |
|
|
|
1915 C.E. |
|
Panama Canal opened |
| 1916
C.E. |
|
Einstein's general theory of relativity |
|
|
|
| 1917
C.E. |
|
Hardy and Ramanujan |
1917 C.E. |
|
Russian Revolution:
The Balfour DeclarationArthur
James
Balfour, 1st earl of Balfour (1848–1930)
Balfour was first lord of the admiralty from 1915 to 1916 in Herbert
Asquith's coalition government and in 1916 became foreign secretary
under David Lloyd George. In this capacity in 1917 he issued the
Balfour Declaration, pledging British support to the Zionist hope for a
Jewish national home in Palestine, with the proviso that the rights of
non-Jewish communities in Palestine would be respected |
|
|
|
1919 C.E. |
|
League of Nations |
|
|
|
1927 C.E. |
|
Lindberg flew the
Atlantic |
|
|
|
1928 C.E. |
|
Fleming discovers
penicillan |
| 1931
C.E. |
|
Gödel's Theorem |
|
|
|
|
|
|
1932 C.E. |
|
Atom split |
|
|
|
1933 C.E. |
|
Hitler became
Chancellor |
| 1936
C.E. |
|
Ahlfors and Douglas
awarded the first Fields
MedalsFields Medal
In 1924 at the International Congress of Mathematicians it was proposed
that gold medals should be awarded to recognize outstanding
mathematical achievement. It wasn't until 1936 that the first medals
were awarded to Lars Valerian Ahlfors (Harvard University) and Jesse
Douglas (Massachusetts Institute of Technology). The Fields Medals are
awarded every four years. This award is considered to be the equivalent
to the Nobel Prize (which does not exist in mathematics). An
interesting restriction is that the medals would not be given to
mathematicians over forty years of age! |
|
|
|
| 1939
C.E. |
|
Volume I of Bourbaki's ElémentsThe
name Nicolas Bourbaki was used to disguise a group of anonymous French
mathematicians who took it upon themselves to revitalize mathematics.
The story of Bourbaki is too complex to summarize briefly. The
following URL gives a nice history of Bourbaki.
http://planetmath.org/encyclopedia/
NicolasBourbaki.html |
|
|
|
|
|
|
1941 C.E. |
|
Pearl Harbor |
|
|
|
1945 C.E. |
|
Bombing of Hiroshima |
|
|
|
1946 C.E. |
|
First meeting of
the U.N. |
|
|
|
1950 C.E. |
|
Korean War began |
|
|
|
1957 C.E. |
|
Sputnik I launced |
|
|
|
1958 C.E. |
|
Berlin airlift |
| 1961
C.E. |
|
Lorenz on chaotic
behaviorEdward Lorenz (1917 - 2008), an American meteorologist at the
Massachusetts Institute of Technology, discovered a simple mathematical
system with chaotic behavior. This discovery led to the new mathematics
of chaos theory which is now widely applicable. |
|
|
|
| 1963
C.E. |
|
Paul J. Cohen on the
continuum hypothesisPaul J. Cohen (1934 - 2007), an American
mathematician, proves the independence of the axiom of choice and of
the continuum hypothesis. For his efforts he won the Fields Medal in
1966. |
1963 C.E. |
|
Assassination of
President Kennedy |
|
|
|
1965 C.E. |
|
Death of Sir
Winston Churchill |
|
|
|
1967 C.E. |
|
Summer of LoveThe
Summer of Love was a designation for the summer of 1967. Hippies from
all over the country flocked to the Haight-Ashbury district of San
Francisco that summer. This is when the hippie movement came to full
fruition. The Mamas and the Papas hailed this event with their song, If
You Go To San Francisco, which began '"If you're going to San
Francisco, / be sure to wear some flowers in your hair... “ |
|
|
|
1969 C.E. |
|
Man walks on the
moon |
| 1970
C.E. |
|
Matiyasevich shows
Hilbert's tenth problem is
unsolvableYuri Matiyasevich (1947 - ), a Russian mathematician,
showed that "Hilbert's tenth problem" was unsolvable, namely that there
is no general method for determining when polynomial equations have a
solution in whole numbers. |
|
|
|
|
|
|
1974 C.E. |
|
President Nixon
resigns |
|
|
|
1975 C.E. |
|
End of Vietnam War |
| 1976
C.E. |
|
Four Color conjecture
verified by computerKen Appel and Wolfang Haken showed that the
Four Color Conjecture is true using 1200 hours of computer time to
examine around 1500 configurations.
The four-color theorem states that any map in a plane can be colored
using four-colors in such a way that regions sharing a common boundary
(other than a single point) do not share the same color. |
|
|
|
| 1977
C.E. |
|
Adelman, Rivest and
Shamir introduce public-key
codesRonald Rivest, Adi Shamir, and Leonard Adleman introduce
public-key codes (known as the RSA algorithm), a system for passing
secret messages using large primes and a key which can be published.
Leonard Adleman (1945 - ) is a theoretical computer scientist and
professor of computer science and molecular biology at the University
of Southern California.
Ronald Linn Rivest (1947 - ) is a cryptographer, and is the Viterbi
Professor of Computer Science at MIT's Department of Electrical
Engineering and Computer Science.
Adi Shamir (1952 - ) is an Israeli cryptographer. |
1977 C.E. |
|
First Star
Wars movie released |
| 1982
C.E. |
|
Mandelbrot's The
fractal geometry of natureBenoit Mandelbrot (1924 - )
publishes The fractal geometry of
nature, which describes the theory of fractals. This study was
largely responsible for the present interest in fractal geometry. He
showed how fractals can occur in many different places in both
mathematics and elsewhere in nature. |
|
|
|
|
|
|
1984 C.E. |
|
Ethiopian famine |
|
|
|
1989 C.E. |
|
Fall of Berlin Wall |
|
|
|
1990 C.E. |
|
Nelson Mandela
released from prison |
|
|
|
1991 C.E. |
|
Soviet Union
disintegrates |
| 1994
C.E. |
|
Wiles proves Fermat's
Last TheoremAndrew Wiles (1953 - )
The proof of Fermat's Last Theorem was first announced in 1993 by
Andrew Wiles, a British mathematician working at Princeton University.
Wiles gave a series of three lectures at the Isaac Newton Institute in
Cambridge, culminating with the announcement that he had proved
Fermat's Last Theorem as a corollary to his main results. However, his
proof was not entirely correct and it was another year before he had
corrected his proof. His paper which proves Fermat's Last Theorem is Modular
elliptic curves and Fermat's Last Theorem which appeared in the
Annals of Mathematics in 1995. |
|
|
|
| 2000
C.E. |
|
Mathematical Challenges
of the 21st Century
announcedIn an effort to duplicate Hilbert's proposed problems of
1900, a team of 30 leading mathematicians, of whom eight were Fields
Medal winners, proposed "Mathematical Challenges of the 21st Century"
at a meeting of the American Mathematical Society in Los Angeles. |
|
|
|
 for one; a heel bone
for one; a heel bone  for 10; a
coil of rope
for 10; a
coil of rope  for 100; a lotus
flower
for 100; a lotus
flower  for 1000; a pointing
finger
for 1000; a pointing
finger  for 10,000; a
borbot fish (or tadpole)
for 10,000; a
borbot fish (or tadpole)  for 100,000; and an astonished man
for 100,000; and an astonished man  for 1,000,000. Clearly their number system was a base ten
system; however, they used a simple grouping system rather than a
positional system.
for 1,000,000. Clearly their number system was a base ten
system; however, they used a simple grouping system rather than a
positional system.