 |
What intrigued me about this problem was the fact that although we were
dealing with a three dimensional solution to the problem, the two
dimensional drawing in Figure 1 made the problem appear solvable in the
plane. This led to the investigation of the case in which the point ![]() is in the plane of
is in the plane of ![]() . More precisely,
given a quadrangle
. More precisely,
given a quadrangle ![]() and a point
and a point ![]() in its
plane, construct a line
in its
plane, construct a line ![]() such that there is a
parallelogram
such that there is a
parallelogram ![]() which is copolar with
which is copolar with ![]() from the point
from the point ![]() and coaxial from the
line
and coaxial from the
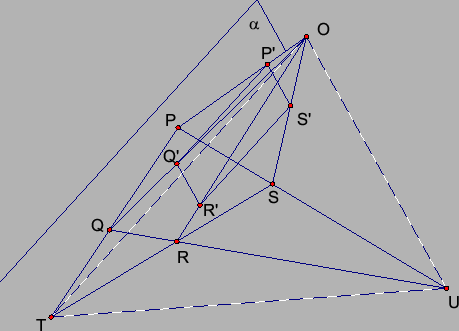
line ![]() . See Figure 2.
. See Figure 2.
If ![]() is in the plane of
is in the plane of ![]() , the construction is
as follows. Join
, the construction is
as follows. Join ![]() with the vertices
with the vertices ![]() and the exterior diagonal points
and the exterior diagonal points ![]() and
and ![]() . On the line
. On the line ![]() pick a
point
pick a
point ![]() and construct lines
and construct lines ![]() and
and ![]() parallel to
parallel to ![]() and
and ![]() , respectively.
, respectively. ![]() meets
meets ![]() in a point
in a point ![]() and
and ![]() meets
meets ![]() in a point
in a point ![]() . Join the
points
. Join the
points ![]() and
and ![]() . The line
. The line ![]() meets
meets ![]() at
at ![]() and
and ![]() at
at ![]() . Join the points
. Join the points ![]() and
and ![]() which meet
which meet ![]() at
at ![]() . Join
. Join ![]() and
and ![]() . This
line intersects
. This
line intersects ![]() at
at ![]() and the figure
and the figure ![]() is the required parallelogram.
is the required parallelogram.
Proof. Triangles ![]() and
and ![]() are coaxial from the line
are coaxial from the line ![]() since
since ![]() meets
meets ![]() in
in ![]() ,
, ![]() meets
meets ![]() in
in ![]() and
and ![]() meets
meets ![]() in
in ![]() . By Desargues'
Theorem, these triangles are copolar. By construction,
. By Desargues'
Theorem, these triangles are copolar. By construction, ![]() is parallel to
is parallel to ![]() . Therefore, the pole
is an ideal point, and thus
. Therefore, the pole
is an ideal point, and thus ![]() is parallel to
is parallel to ![]() . Since triangles
. Since triangles ![]() and
and ![]() are coaxial from line
are coaxial from line ![]() , we see, by a
similar argument, that
, we see, by a
similar argument, that ![]() is parallel to
is parallel to ![]() . All that remains to prove is that
. All that remains to prove is that ![]() and
and ![]() are concurrent at
are concurrent at ![]() .
.
Suppose ![]() meets
meets ![]() at
at ![]() . Triangles
. Triangles ![]() and
and ![]() are coaxial from the line
are coaxial from the line ![]() , and therefore they
must be copolar. Line
, and therefore they
must be copolar. Line ![]() was constructed parallel to
was constructed parallel to ![]() ; therefore
; therefore ![]() is parallel to
is parallel to ![]() . On the other hand, it has already been established that
. On the other hand, it has already been established that ![]() is parallel to
is parallel to ![]() . Since one and only
one line can be drawn parallel to a given line through a given point,
. Since one and only
one line can be drawn parallel to a given line through a given point, ![]() is on line
is on line ![]() . Therefore, lines
. Therefore, lines
![]() are concurrent on
are concurrent on ![]() .
.
It is worth noting that if ![]() is chosen to be on
the circle with diameter
is chosen to be on
the circle with diameter ![]() , the parallelogram
, the parallelogram ![]() will be a rectangle.
will be a rectangle.
Moreover, it appears that there exist points on the circle for which
the rectangle becomes a square. Below, in Figure 4, we see rectangles
that are produced by choices of ![]() close to
close to ![]() and close to
and close to ![]() . In the drawing on the left
. In the drawing on the left ![]() ; whereas, on the right
; whereas, on the right ![]() .
As
.
As ![]() moves from the position on the left to the position on the
right, the dimensions of the rectangle change continuously from
moves from the position on the left to the position on the
right, the dimensions of the rectangle change continuously from ![]() to
to ![]() . In Figure 5 we see
. In Figure 5 we see ![]() near a point that produces a square.
near a point that produces a square.
This document was generated using the LaTeX2HTML translator Version 2002-2-1 (1.70)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The translation was initiated by Bill Richardson on 2007-04-16