At the beginning, we saw the 33 lo-shu magic square. By the way, the old Chinese way of representing numbers was with knots on a string. They would use white knots when creating an odd number and black dots when creating an even number. The lo-su in the old Chinese number system looked like this:

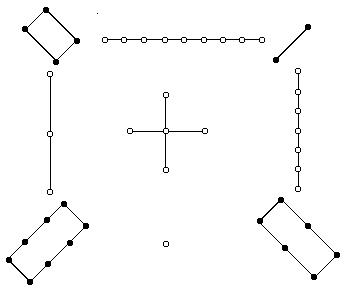
Being an odd ordered magic square, the lo-shu can be constructed using the method described in the material on odd-ordered magic squares and flipping the square through a horizontal axis. Another way to construct the lo-shu magic square is given in the following illustration.

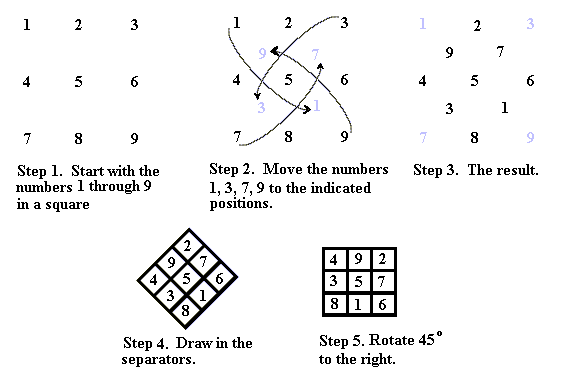
Since the 33 magic square is small in the number of numbers that appear in it, we can easily establish some special properties.

Property 1. The only number that can appear in the center of the 33 magic square is 5.

Proof. Suppose we try the other numbers. We first note that the number that is in the middle cell of the square requires that there be four distinct pairs that sum to 15 with the center number as we see in the figure below.

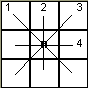
If 1 is in the center square we then need to find four pairs of integers from the set {2,3,4,5,6,7,8,9} such that each pair sums to 14 (If 1 is in the center, there will be one column containing 1, one row containing 1 and both diagonals.). There are only two such pairs (5,9) and (6,8), so 1 cannot be in the center.

If 2 is in the center, then we need four pairs that sum to 13; however, there are only three such pairs (4,9), (5,8) and (6,7). Thus, 2 cannot be in the center square.

If 3 is in the center square, then we need four pairs that sum to 12. The pairs that sum to 12 are (4,8), and (5,7). Note: We cannot use the pair (3,9) because 3 is already being used and we can only use 6 once so there is no (6,6) pair available.. Hence, 3 cannot be in the center.

Finally, if 4 is in the center, then we need four pairs that sum to 11. There are only three pairs that sum to 11. They are (2,9), (3,8) and (5,6). Therefore, 4 cannot be in the center and that leaves the only possible center number to be 5.

Property 2. No corner cell can contain an odd integer.

Proof. Without loss of generality, we can restrict our attention to the upper-left corner cell. Suppose that cell contains 1. We now know that 5 must be in the center cell, so the number in the diagonally opposite cell from 1 must be 9. Now, in order to sum to 15 the top row must contain the numbers 1, 6, and 8. If either the 6 or 8 is in the corner cell then, since that column has 9 in its bottom cell, the sum of that column is more than 15. Tis same aregument will also show that 9 cannot be in a corner.

Suppose the upper-left corner contains 3. Then its opposite cell must contain 7, since 3 + 5 + 7 = 15. That means the upper row must be the numbers 3, 4 and 8. If 8 is in the upper-right corner, the summ of that column will be 7 + 8 + ? which will be more than 15. If 4 is in the corner, then we would have 4 + 7 + ? = 15 and the only number that will fit is 4 which is already used. This argument also shows that 7 cannot be in a corner.

The above two properties determine that all magic squares of order come from the same square by rotations and reflections. Once we establish that 5 must be in the center and no odd integer can be a corner, we have that the even integers must be the corners and they must be paired so that 2 and 8 are diagonally opposite of each other with 5 in the middle and 4 and 6 must be diagonally opposite of each other with 5 in the middle. This immediately fixes 1, 3, 7, and 9. The 1 must be between 8 and 6, 3 must be betwee 8 and 4. Thus, 7 must be between 2 and 6 and 9 must be between 2 and 4.

Below is the lo-shu and its three rotations. The rotations are to the left 90°, 180°and 270°.

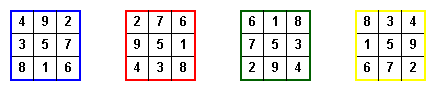
If we then reflect each of these through the center column, we get

Reflections through the center row give no new arrangements, as one can easily verify. Likewise, no reflection through a diagonal will yield a new square.