Some fun magic squares are created using magic squares as the elements of other magic squares. For example we can create a 5![]() 5 magic square in which the elements are 3
5 magic square in which the elements are 3![]() 3 magic squares. The square will be a 15
3 magic squares. The square will be a 15![]() 15 magic square using the numbers 1, 2, 3, ... , 225. We create the magic square by first building twenty-five 3
15 magic square using the numbers 1, 2, 3, ... , 225. We create the magic square by first building twenty-five 3![]() 3 magic squares using the sets {1, 2, 3, ..., 9}, (10, 11, 12, ..., 18}, ..., {215, 218, 219, ..., 225}. That is,
3 magic squares using the sets {1, 2, 3, ..., 9}, (10, 11, 12, ..., 18}, ..., {215, 218, 219, ..., 225}. That is,
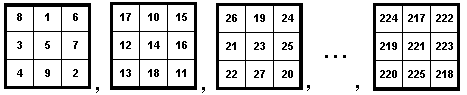
We then build a 5![]() 5 magic square using these twenty-five 3
5 magic square using these twenty-five 3![]() 3 magic squares as the elements. The 3
3 magic squares as the elements. The 3![]() 3 magic squares and the 5
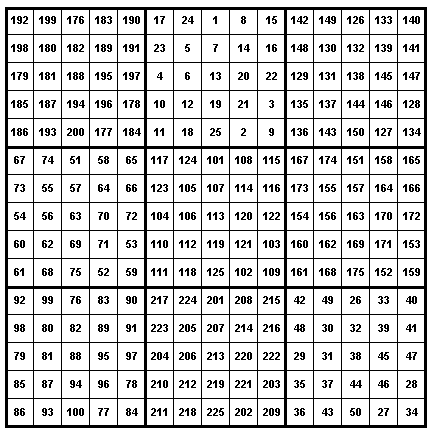
3 magic squares and the 5![]() 5 magic square are constructed in the usual way for an odd-ordered magic square. The result is the following magic square
5 magic square are constructed in the usual way for an odd-ordered magic square. The result is the following magic square
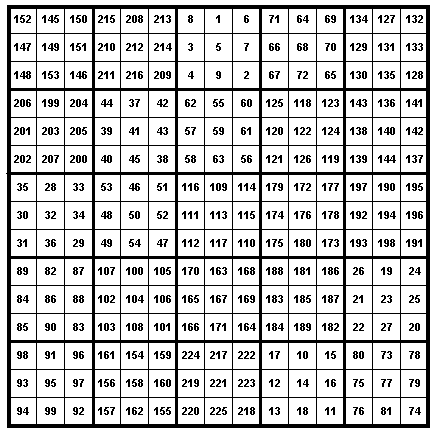
If we replace each of the 3![]() 3 magic squares by their magic numbers, we get a 5
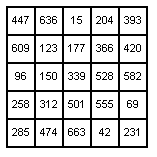
3 magic squares by their magic numbers, we get a 5![]() 5 magic square using the twenty-five numbers in the arithmetic progression {15 + 27*k} for k = 0, 1, 2, ..., 24. That is, the numbers
5 magic square using the twenty-five numbers in the arithmetic progression {15 + 27*k} for k = 0, 1, 2, ..., 24. That is, the numbers
This would give us the magic square
We can construct magic squares of any order with elements that are also magic squares. We would use the same methods as we do for regular magic squares. An example of a 3![]() 3 magic square with elements that are 4
3 magic square with elements that are 4![]() 4 magic squares is given below.
4 magic squares is given below.
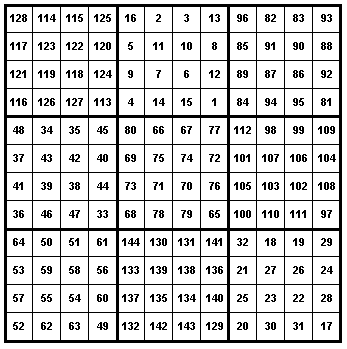
An example of a 3![]() 3 magic square with elements that are 5
3 magic square with elements that are 5![]() 5 magic squares is given below.
5 magic squares is given below.
Try some of your own.
| Magic Squares -- Introduction | Magic Squares of Order 3 | 4th Order Magic Squares | Magic Squares of Order 4n | Magic Squares of Odd orders | Magic Squares of Even orders--4n+2 | Ben Franklin's Magic Square | Magic Squares which are not Normal |