Day 4

John Hammond

Sketch 12: A Cheerful Fact: The Pythagorean Theorem

A Mesopotamian question:

A translation of a Babylonian tablet which is preserved in the British museum goes as follows:

4 is the length and 5 the diagonal. What is the breadth ? Its size is not known. 4 times 4 is 16. 5 times 5 is 25. You take 16 from 25 and there remains 9. What times what shall I take in order to get 9 ? 3 times 3 is 9. 3 is the breadth.

Plimpton 322

Plimpton 322

Plimpton_322.jpg1

Plimpton 322

plimpton322-fig4-eves.jpg

Figure 1: Numeric translation in (Eves, 1990)

Seemingly unrelated fact:

  • A Pythagorean triple is a set of three numbers which satisfy the Pythagorean theorem.
  • A primitive Pythagorean triple is a triple in which all three numbers have no common factors other than one.
  • Example: …
  • Non-example: …

Seemingly unrelated fact:

  • A general fact is that all primitive Pythagorean triples, \(a, b, c\) are given by the expression: \(a = 2uv, \hspace{2em} b = u^2 - v^2 , \hspace{2em} c = u^2 + v^2\)
  • where:
  • \(u\) and \(v\) have no common factors other than 1,
  • one or the other is even while the other is odd, and
  • \(u > v\)
  • Examples.

Back to Plimpton

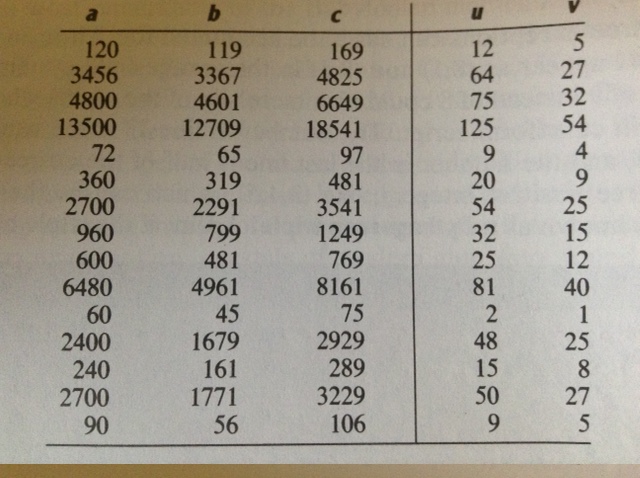
Tables from (Eves, 1990, pp. 45, 46)

  • Seems plausible: the numbers \(u\) and \(v\) (and so \(a=2uv\)) of the form \(n=2^a 3^b 5^c\) for non-negative integers \(a, b,c\)

Back to Plimpton

Plimpton_322.jpg1

Back to Plimpton

  • What about column 4?
  • Entries in column 4 correspond to \((c/a)^2\).
  • What is \(c/a\) for a general right triangle?
    • the secant of a base angle
    • Going down the table, (Eves, 1990) points out the value “decreases by almost exactly 1/60 as we pass from one line of the table to the next, and the corresponding angle decreases from \(45^\circ\) to \(31^\circ\).”
  • We have a secant table! in 1800BCish.

Plimpton 322 - Counter Views

  • First - Sherlock Holmes in Babylon (Buck, 1980)
    • Fascinating case
    • Mysterious clues
  • Eleanor Robson - Neither Sherlock Holmes Nor Babylon (Robson, 2001)
  • Not Sherlock Holmes:
    • Math is written by people
      • We need to view in historical setting
      • Not just “cherry-pick the ‘cleverest’ or ‘most-sophisticated’ mathematical procedures”.
    • Can’t just deduce like a locked room mystery
      • :-(

Plimpton 322 - Counter Views

  • Nor Babylon:
    • The tablet is from 60 years before Hammarabi takes Babylon and creates Babylonia - … though this is a pedantic argument of the original author’s creative choice of words…
  • Argues against Pythagorean triples
  • Very against the trig table
    • No record of use of angle measurement
  • In favor of a table of reciprocals

Plimpton 322 - Pro Views

  • The most recent work is August 2017 (Mansfield & Wildberger, 2017)
    • argues that it is an exact ratio-based trig table
    • no reliance on angles.
    • … due to use of base 60, no need to approximate fractions

Chinese(?) Pythagorean Theorem

In the Zhoubi Suanjing (translated The Arithmetic Classic of the Gnomon and the Circular Paths of Heaven)

Here is a photo of a Ming dynasty 1603 copy:

zhoubijing.jpg

And here is a more modern focused image

Chinese_Pythagoras.jpg

  • This is functionally similar to Thabit Ibn Qurra’s proof without words mentioned in (Berlinghoff & Gouvêa, 2015)
    • (Chemla, 2005) notes that the two proofs are distinct in the manner of the interpretation of the diagrams.
      • Thabit physically moves the pieces to construct two ’unequal squares’
      • Liu Hui (commenting on the Zhou work) viewed it as two different ways to construct the same physical area (note that the external triangles are likely a drawing aid and not used in the proof, according to Chemla)
  • As an aside, (Eves, 1972) attributes this to Bhaskara; I haven’t traced that down further.
  • Let’s take a look at the proof Head to Geogebra!

Pythagorean Number Theory

  • Pythagoreans loved numbers!
  • Special number properties (composite numbers)
  • Pythagorean triples (from Mesopotamia?)
  • Triangular, square, pentagonal, etc. numbers
  • “Perfect” numbers (along with “Deficient” and “Abundant” numbers)
  • “Amicable”/“Friendly” numbers2

Sum of odd numbers

(Opposite of) a homework question, did you notice the sum of odd numbers?

Examples of Figurate Numbers

  • Triangular Numbers: \(1, 3, 6, 10, 15, 21, \dots\)
    • The third triangular number, denoted \(T_3\), is 6.
  • Square Numbers: \(1, 4, 9, 16, 25, \dots\)
    • The fourth square number, \(S_4\), is 16.
  • Pentagonal numbers: \(1, 5, 12, 22, 35, \dots\)
    • The second pentagonal number, \(P_2\), is 5

Pentagonal_number.gif 3

Figurate number relations

  • Square in terms of triangular numbers
  • Square in terms of “gnomons”
  • from Pythagoras, according to Proclus (Heath, 1921):
    • Take a square number that is odd
    • Add this to the square which is the sum of all preceding odd numbers.
    • This makes the square of all odd numbers up to the original
      • \(m^2 + \left( \dfrac{m^2 -1}{2} \right)^2 = \left(\dfrac{m^2 +1}{2}\right)^2\)
  • Pentagonal numbers in terms of squares and triangles

Perfect, Abundant, Deficient

  • First, we need to be comfortable with finding divisors:
    • What are the divisors of: 6? 18? 28? 39?
  • Proper divisors are those divisors which are not equal to the number itself.
  • A perfect number one that equals the sum of its proper divisors.
    • After we talk about Euclid, we might come back to this. It’s remarkable!
  • An abundant number is one such that the sum of the proper divisors is greater than the number.
  • A deficient number is one such that the sum of the proper divisors is less than the number.

Amicable Numbers

  • What are the proper divisors of 220 and 284?
  • 220:
    • 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 and 110
  • 284:
    • 1, 2, 4, 71 and 142
  • What neat thing do you observe?