 |
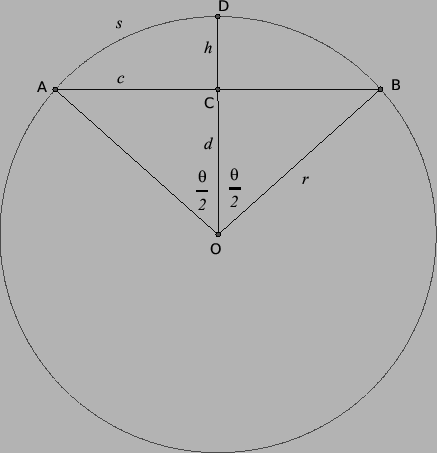
In the figure above ![]() is the chord of the circle,
is the chord of the circle, ![]() is the arc length
is the arc length ![]() ,
, ![]() is the
radius,
is the
radius, ![]() is the central angle determined by the chord
is the central angle determined by the chord ![]() ,
, ![]() is the distance from the chord to the circle
and
is the distance from the chord to the circle
and ![]() is the distance from the center of the circle to the
chord. The following relationships hold:
is the distance from the center of the circle to the
chord. The following relationships hold: ![]() ,
,
![]() ,
,
![]() and
and ![]() .
From these we get
.
From these we get
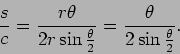 |
(1) |
| (2) |
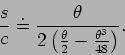 |
(3) |
| (4) |
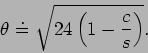
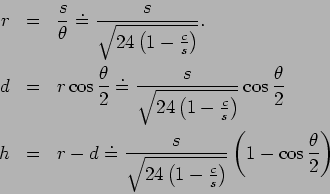
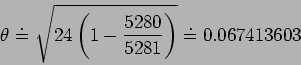

Is that surprising, or not?
This document was generated using the LaTeX2HTML translator Version 2002-2-1 (1.70)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The translation was initiated by Bill Richardson on 2007-04-18