Here we will generalize the method used to generate fourth-order magic squares to generate squares of order 4n. That is, squares for which the number of cells on a side is a multiple of 4.

We can use almost the same process as we used to generate a fourth-order magic square to create any 4n4n magic square. For example to create an 88 magic square. Again we begin with a square matrix of size 88 and draw all the diagonals in the four 44 block that make up the matrix to get.

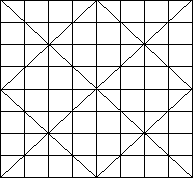
We proceed as we did in the 44 case, but this time we will be using all the positive integers from 1 to 64. We start in the upper left-hand corner to put numbers in the cells. As before, we will only put the cell number in the cell if the cell is blank; that is, does not have a diagonal line in it. We continue this process until we reach the lower right-hand corner. Our square would then look like this:

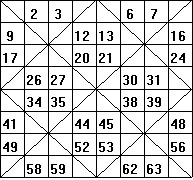
Now we begin in the lower right-hand corner and work our way back using the numbers 1,4,5,8,10,11,... and 64. We put these number in the cells which originally had the diagonal lines starting with 1 in the lower right-hand corner. Our finished product looks like this:

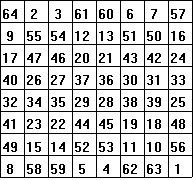
The magic number is 260 = 8(8² + 1)/2. You can check all the rows, columns and diagonals to see that they each have a sum of 260.

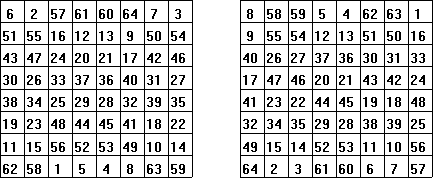
Again, we could get new squares by carefully rearranging the rows and columns of the one above. As before, we must take care to make sure that the numbers that are associated together in all rows and columns stay together. A random exchange of rows or columns will not necessarily result in a new magic square. The rows and columns may sum to 260, but the diagonals may not. Below are two rearrangements of our original 88 magic square.

A 1616 magic square can be constructed in the same way. We start with a 1616 square matrix and draw the diagonals in he 1616 square and the 88 squares and the 44 squares to get a starting square as follows.

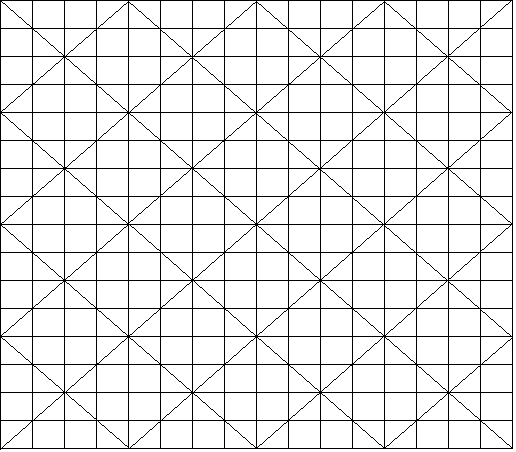
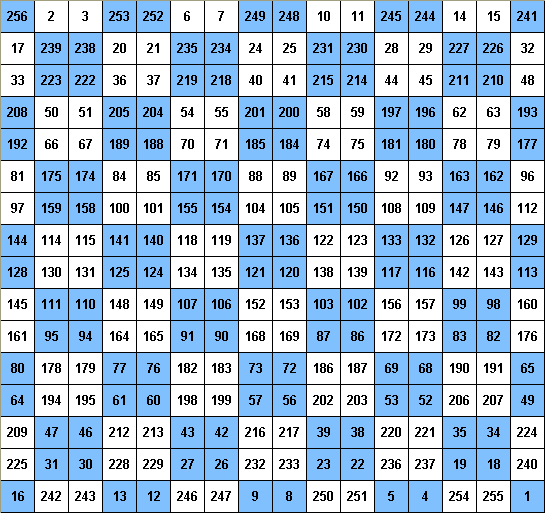
We again start in the upper left-hand corner and fill in the blank squares as before -- except now we use the integers from 1 to 256 (16²). When we finish in the lower right-hand corner, we then proceed backwards filling in the squares that were not used before. The following square is complete with the colored squares being the ones in which diagonal lines had appeared. Notice that the rows, columns and diagonals sum to the magic number 16(16² + 1)/2 = 2056.

The reader can now construct a 1212 magic square. The initial diagonal pattern would be

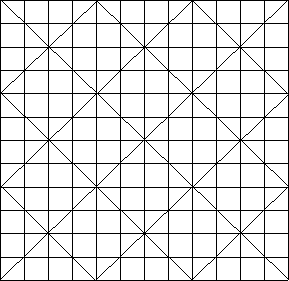
Use the numbers from 1 to 144. Your magic number will be 12(12² + 1)/2 = 870. Have fun!

There is another method, similar to the above, that can be used to generate 4n4n magic squares. The squares generated will not be the same as the ones generated by the above method. Instead of crossing out cells with diagonals, we subdivide the square with squares and rectangles that are determined by the size of the square. The method, often called "the nine-block method", is as follows.

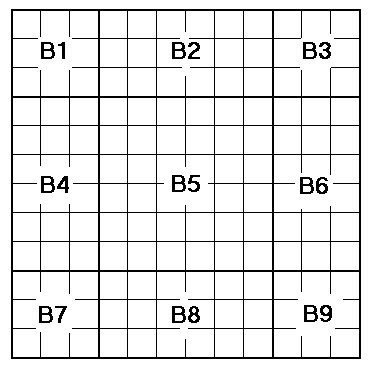
First we partition the nn square into nine blocks B1, B2, ..., B9 as follows: four n/4n/4 squares B1, B3, B7, and B9 at the corners, a n/2n/2 square, B5, in the center and the remaining four rectangles, two n/4n/2, B4 and B6, and two n/2n/4, B2 and B8. We illustrate with a 1212 square.

We can then proceed in one of two ways.

Method 1. Number the cells 1 through n² (in our case, it would be 1 through 144). Leave the numbers as they are in the five squares.

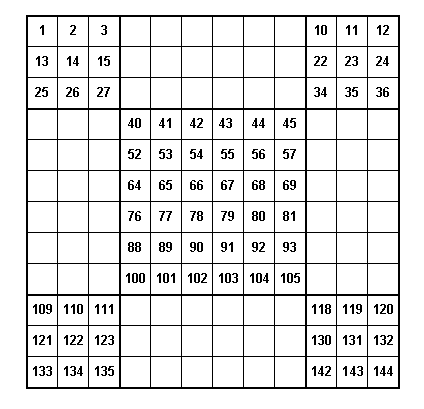
Then start at the bottom as we did in our first way of generating 4n4n magic squares and enter the cell values in the rectangles as we count from bottom to top. This would give the magic square.

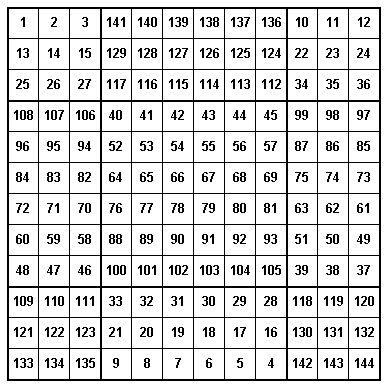
If one is fast at calculations, one could compute the values that goes in each cell. If we let r represent the row number and c represent the column number for each cell in the square. Then the values that would go in the cells in the square blocks would be (r - 1)*n + c and the values that go in the rectangular blocks would be (n² + 1)-[(r - 1)*n + c]. For example, in our 1212 square above the value in the 7^th row and 5^th column would be in the middle square, block B5, and it would be (7 - 1)*12 + 5 = 77. The element in the 8^th row, 11^th column would be (144 + 1) - (8 - 1)*12 + 11 = 145 - 95 = 50.

Method 2. If we enter the numbers in every cell in order, we get

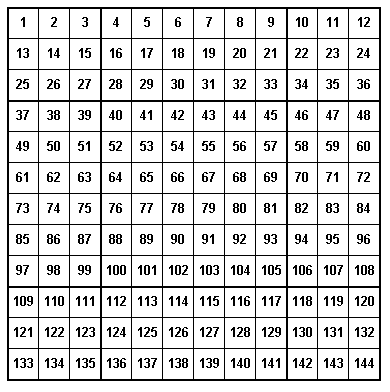
We then remove the rectangular blocks, B2, B4, B6, B8. Now we take B2 and rotate it 180º and place it where B8 was and rotate the original block B8 180º and put it where B2 was. We then do the same with blocks B4 and B6. We rotate each 180º and put it where the other was and we again get the square