A magic square of order n was said to be normal if it was magic and the numbers 1, 2, 3, ... , n2 are used in the cells.
Other, non-normal magic squares can be easily constructed using the rules we have described in the other pages with the entries being elements of an arithmetic progression. For example, we could construct a 3
3 magic square using the numbers 4,8,12,16,20,24,28,32,36.
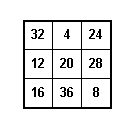
The magic number in this case is (4+8+12+16+20+24+28+32+36)/3 = 60, or since each if teh numbers 1,2,...,9 is multipled by 4, the magic number is just 4 times the magic number for the normal 33 magic square.
An arithmetic progression is a sequence of numbers of the form a + (k - 1)d, k=1,2,3,...,n, where a is the first term and d is the constant difference between terms. The difference between any two consecutive terms of an arithmetic progression is constant. Interesting magic squares can be created using arithmetic progressions that may seem to hide the pattern. For example, suppose we consider the arithmetic progression given by 7 + 3(k-1), k = 1, 2, 3, ..., 16. These would be the numbers 7, 10, 13, 16, ..., 52. If we create the 44 magic square using these numbers, we have the following magic square with magic number 118.
Try some of your own.
| Magic Squares -- Introduction | Magic Squares of Order 3 | 4th Order Magic Squares | Magic Squares of Order 4n | Magic Squares of Odd orders | Magic Squares of Even orders--4n+2 | Ben Franklin's Magic Square | Magic Squares within Magic Squares |