Magic Squares
of Order 3

Magic Squares
of Order 4

Magic Squares
of Order 4n

Magic Squares
of Odd orders

Magic Squares
of Even orders (4n+2)

Magic Squares which are not Normal

Ben Franklin's Magic Square

Magic Squares within Magic Squares

Magic squares have been known for many centuries. The standard or normal magic square is defined as an arrangement of the first n² natural numbers (or positive integers) into a square matrix so that the sum of the numbers in each column, row and diagonal is the same magic number. This magic number is determined by n and is equal to n(n² + 1)/2. The number n, the number of cells on one of the sides of a magic square is referred to as the order of the magic square.

Here is one of the earliest known magic squares.

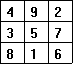
It is a 3x3 square using the numbers 1, 2, 3, ..., 9. Notice that each row, column and diagonal sums to the magic number 15 = 3(3² + 1)/2. This magic square may possibly date back as early as 2200 B.C. in Chinese history. It is called  lo-shu  and is considered a lucky charm.

Another historical note concerning magic squares of order 4. The earliest recorded fourth-order magic square appears to have been found in an inscription at Khajuraho, India dating to about 1000-1100 A.D. It was of the form

As we amble through this topic, we will see how to construct some magic squares as well as look at some magic squares of historical significance. We will also examine some very special almost-magic squares created by Ben Franklin. Franklin's squares are not true magic squares, in that the diagonals do not sum to the magic number. However, other interesting combinations in his squares sum to the magic number.

If one is interested is pursuing further study of magic squares, then you should visit the following site which has a very large data base and many, many links. Rather than trying to generate a list myself, I refer you to Professor Mutsumi Suzuki's page.