We have examined even ordered magic squares with orders equal to a multiple of 4. These are often referred to as doubly-even magic squares. We will now look at magic squares that are of even order where the order is not a multiple of 4. These would have order 6, 10, 14, ... That is, numbers that are 2 times and odd number. 2(2n+1) = 4n + 2. We can easily show that there are no 2![]() 2 magic squares. The magic number would be 5 and no matter how we arranged the numbers 1, 2, 3, 4 in a square matrix, we cannot get all rows, columns and diagonals to sum to 5. Note each of the four numbers would be a corner and hence 1 would be a corner and would require three different numbers to sum with it and get 5--which is impossible.
2 magic squares. The magic number would be 5 and no matter how we arranged the numbers 1, 2, 3, 4 in a square matrix, we cannot get all rows, columns and diagonals to sum to 5. Note each of the four numbers would be a corner and hence 1 would be a corner and would require three different numbers to sum with it and get 5--which is impossible.
A 6![]() 6 magic square is then the first to have order 4n + 2. The following is a 6x6 magic square.
6 magic square is then the first to have order 4n + 2. The following is a 6x6 magic square.
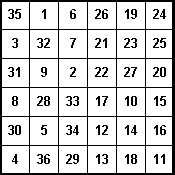
We will examine the way this particular 6![]() 6 magic square was generated. The are other methods, but as we will see they are not as straightforward as the methods we showed for odd ordered magic squares and doubly-even ordered magic squares. However, the way the above square was generated is rather intriguing.
6 magic square was generated. The are other methods, but as we will see they are not as straightforward as the methods we showed for odd ordered magic squares and doubly-even ordered magic squares. However, the way the above square was generated is rather intriguing.
First we partition the 6![]() 6 matrix into four 3
6 matrix into four 3![]() 3 blocks. In the upper left-hand block we enter the numbers 1,2,3,...,9 by the Siam method. (See the figure below.) We then enter the numbers 10,11,12,...,18, using the Siam method, in the lower right-hand block. Next we enter the numbers 19,20,21,...,27 in the same way in the upper right-hand block. Finally, we enter the numbers 28,29,30,...,36 in the lower left-hand block, getting the square at right in the figure below.
3 blocks. In the upper left-hand block we enter the numbers 1,2,3,...,9 by the Siam method. (See the figure below.) We then enter the numbers 10,11,12,...,18, using the Siam method, in the lower right-hand block. Next we enter the numbers 19,20,21,...,27 in the same way in the upper right-hand block. Finally, we enter the numbers 28,29,30,...,36 in the lower left-hand block, getting the square at right in the figure below.
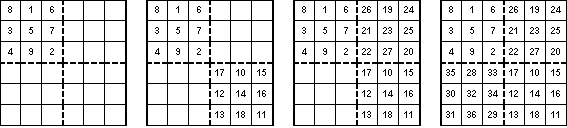
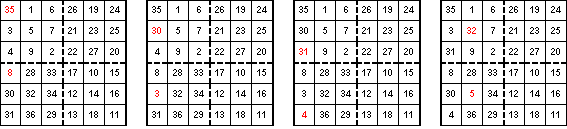
We check this last square and find that all the columns sum to the magic number 111 = 6(62 + 1). However, the rows do not sum to 111. In fact the first three rows sum to 84 and the last three sum to 138. What can we do to correct this? First of all if we change an element in row one, it must be exchanged with another element in the same column to maintain the sum of 111. In order to get a sum of 111 in row one, we must increase the value of an element in that row by 27, since 111 - 84 = 27. We have three choices. Any one of the first three entries in row one can be exchanged with their corresponding entry in row four. For example, we could exchange the 8 in row one with the 35 in row four. (See the figure below.) We now have rows one and four with sum 111 without changing the sum of column one. We next try exchanging the 3 in row two with the 30 in row five. Again we have success, in that the sums of rows two and five are now 111. Finally we exchange the 4 in row three with the 31 in row six to get the third square in the figure below. Now all the rows and all the columns sum to the magic number 111. However, we have a problem. The diagonals do not sum to 111. We need to switch two elements that are on the diagonals and in the same column. We see that if we return the 3 and 30 to their original places and in column two exchange the 5 and 32, which are diagonal elements,, we have not changed the row sums or column sums, but we have changed the diagonals to now sum to 111 each. The last square in the figure below is the desired magic square of order 6.
The above method is more complicated than the methods we used for previous squares, but once one sees what is happening it is really not too bad.
Let's see if we can adapt this method to a 10![]() 10 square. If we partition the square into four 5
10 square. If we partition the square into four 5![]() 5 squares and put the numbers 1,2,...,25 in the upper left-hand square by the Siam method, the numbers 26,27,..,50 in the lower right-hand square, then numbers 51,52,...,75 in the upper right-hand square and, finally, the numbers 76,77,...,100 in the lower left-hand square, then we get the square below.
5 squares and put the numbers 1,2,...,25 in the upper left-hand square by the Siam method, the numbers 26,27,..,50 in the lower right-hand square, then numbers 51,52,...,75 in the upper right-hand square and, finally, the numbers 76,77,...,100 in the lower left-hand square, then we get the square below.
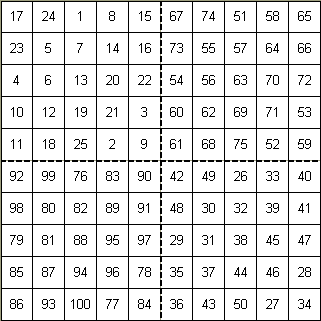
Again, as in the case with the 6![]() 6, the columns sum to the magic number 505 but the rows do not. The switches for this square are not as easily determined as before. Once we see what they are, we will be able to make an informed guess as to what needs to be done in the 14
6, the columns sum to the magic number 505 but the rows do not. The switches for this square are not as easily determined as before. Once we see what they are, we will be able to make an informed guess as to what needs to be done in the 14![]() 14 magic square. For the 10
14 magic square. For the 10![]() 10 square, what we need to do first is exchange the corresponding elements in the upper and lower squares in the first and tenth columns. Then in column two we exchange corresponding elements in the upper and lower squares except for rows three and eight. Then we exchange elements in rows three and eight in column three to get the following magic square of order 10.
10 square, what we need to do first is exchange the corresponding elements in the upper and lower squares in the first and tenth columns. Then in column two we exchange corresponding elements in the upper and lower squares except for rows three and eight. Then we exchange elements in rows three and eight in column three to get the following magic square of order 10.
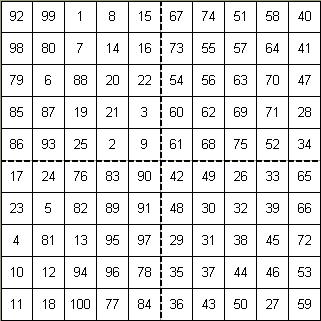
Let's see if we can maybe guess the pattern for a general (4n+2)![]() (4n+2) magic square. 6 = 4*1 + 2, so n = 1 and we changed elements in column one, except for the two diagonal elements. 10 = 4*2 + 2, so n = 2 and we changed element in the first two columns, except for the diagonal elements, and the last column. Since 14 = 4*3 + 2 and n = 3, we might guess that if we change the first three columns, except for the diagonal elements, and the last two rows, we might get a 14
(4n+2) magic square. 6 = 4*1 + 2, so n = 1 and we changed elements in column one, except for the two diagonal elements. 10 = 4*2 + 2, so n = 2 and we changed element in the first two columns, except for the diagonal elements, and the last column. Since 14 = 4*3 + 2 and n = 3, we might guess that if we change the first three columns, except for the diagonal elements, and the last two rows, we might get a 14![]() 14 magic square. If that works, we might figure the rule is in a (4n+2)
14 magic square. If that works, we might figure the rule is in a (4n+2)![]() (4n+2) square, we would change the first n columns, except for the diagonal elements, and the last n-1 columns. Applying this rule to the 14
(4n+2) square, we would change the first n columns, except for the diagonal elements, and the last n-1 columns. Applying this rule to the 14![]() 14 square we get the following square, which is magic.
14 square we get the following square, which is magic.

So, in general, if we want to create a magic square of order n = 4k + 2, then we begin by partitioning the square into four (2k+1)![]() (2k+1) squares. In the upper left square we place, using the Siam method, the integers 1,2,3,...,n2/4. In the lower right-hand square we place the numbers n2/4+1,n2/4+2,...,n2/2, again using the Siam method. In the upper right-hand square we place the numbers n2/2+1, n2/2+2,...,3n2/4, using the Siam method and finally in the lower left-hand square we place the numbers 3n2/4+1,3n2/4+2,...,n2 using the Siam method. Next, in the first k-1 columns and in the last (k-1) columns we exchange the corresponding elements in the upper square with those in the lower square and in the kth column we exchange all but the middle elements of this column. Finally we exchange the middle element of the upper and lower squares in the (k+1)st column. The result should be an nxn magic square.
(2k+1) squares. In the upper left square we place, using the Siam method, the integers 1,2,3,...,n2/4. In the lower right-hand square we place the numbers n2/4+1,n2/4+2,...,n2/2, again using the Siam method. In the upper right-hand square we place the numbers n2/2+1, n2/2+2,...,3n2/4, using the Siam method and finally in the lower left-hand square we place the numbers 3n2/4+1,3n2/4+2,...,n2 using the Siam method. Next, in the first k-1 columns and in the last (k-1) columns we exchange the corresponding elements in the upper square with those in the lower square and in the kth column we exchange all but the middle elements of this column. Finally we exchange the middle element of the upper and lower squares in the (k+1)st column. The result should be an nxn magic square.
| Magic Squares -- Introduction | Magic Squares of Order 3 | 4th Order Magic Squares | Magic Squares of Order 4n | Magic Squares of Odd orders | Magic Squares which are not Normal | Ben Franklin's Magic Square | Magic Squares within Magic Squares |