4th Order Magic Squares

Fourth-order Magic Squares

As a reminder, we should mention here that the order of a magic square is the number of cells on one of its sides.

Recall that the earliest recorded fourth-order magic square appears to have been found in an inscription at Khajuraho, India dating to about 1000-1100 A.D. It was of the form

We will examine a method to create a 44 magic square; however, this method does not generate the square found in India. (This is not the only way, but it is quick and sure.) We begin by creating a 44 square matrix and then we draw two diagonal lines to get a figure as follows.

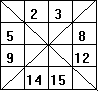
We then start at the upper left corner to put the number 1,2,3,...,14,15,16 into the cells. However, we do not put a number in any cell where the diagonal line appears. We start with 1, but that cell has a diagonal line in it, so we go to the next cell which is blank and enter a 2, then we put a 3 in the next cell. The last cell in the first row has a diagonal line, so we do not write in the 4. We go to the next row and enter 5 in the first cell, which is blank, the next two cells have a diagonal line, so we skip 6 and 7. We continue this pattern until we get to the last cell in the last row. Our square will look like this:

Now we begin in the lower right-hand corner and work our way back using the numbers 1,4,6,7,10,11,13, and 16. We put these number in the cells which originally had the diagonal lines starting with 1 in the lower right-hand corner. Our finished product looks like this:

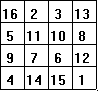
We see that in our finished square every row, column and diagonal sums to the magic number 34, which is found, as we mentioned above, by calculating 4(4² + 1)/2.

Once we have this square, we can carefully rearrange the rows and columns to get other 44 magic squares. Below are some rearrangements of our original 44 magic square.

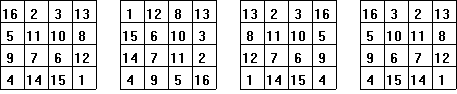
Notice in the rearrangement that the numbers in our original 44 magic square stay together. That is, the numbers 16,2,3,13 that appear in the first row will always be together, in some order, in a row or column of a new square. This is true of all of the other sets of four numbers. For example, if you have a row or column that contains the numbers 3 and 6, that row or column must also have the numbers 10 and 15.

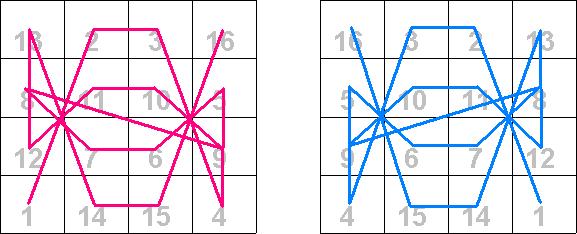
In our rearranged examples above, the last magic square is of particular historical interest in mathematics and art. This magic square appears in the background of the engraving Melencolia by Albrecht Dürer, which he did in 1514. Notice the numbers 15 and 14 (the date of the engraving) appear together in the center of the bottom row. This engraving can be seen in many places. A convenient one is the WebMuseum. If this link does not get you there try the front door. The main entry point to the WebMuseum is the Pyramide.

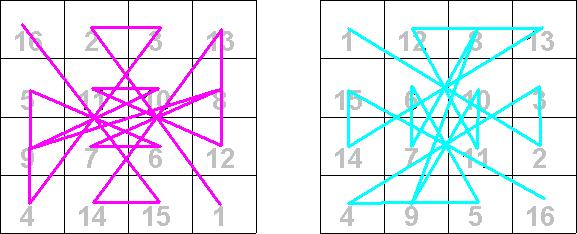
Another observation one can make from these magic squares is the pattern one can get if one traces the position of the numbers 1 through 16 from cell to cell. This was first suggested by Claude Fayette Bragdon, a prominent U.S. architect who lived from 1866 to 1946. Below are the four 44 magic squares given above with the paths traced by colored lines. Notice the symmetries that appear.