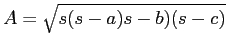 where
where
My guess was that there would be an infinite number of them and it seemed to me that the obvious way to attack this problem was to use Heron's formula for the area of a triangle.
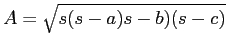 where
where ![]() are the lengths of the three sides of the triangle and
are the lengths of the three sides of the triangle and
![]() . I let the sides of the triangle be represented by the three consecutive integers
. I let the sides of the triangle be represented by the three consecutive integers
![]() . I then found, after simplification, that
. I then found, after simplification, that
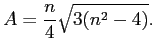 |
(1) |
Upon examination of this result it was clear that ![]() had to be an even integer in order for
had to be an even integer in order for ![]() to be an integer. For if
to be an integer. For if ![]() were odd,
were odd, ![]() would be odd and even if
would be odd and even if ![]() were a perfect square,
were a perfect square, ![]() would not divide
would not divide
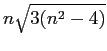 . Also, by observation, it is clear that
. Also, by observation, it is clear that ![]() must be equal to a number of the form
must be equal to a number of the form ![]() . I did a quick search and found that the integers
. I did a quick search and found that the integers ![]() all worked. Since my assumption was that there were going to be an infinite number of these triangles, I looked for a recurrence relation for which
all worked. Since my assumption was that there were going to be an infinite number of these triangles, I looked for a recurrence relation for which ![]() were the first three terms that generated and infinite sequence of values for
were the first three terms that generated and infinite sequence of values for ![]() satisfying (1). I would then test this sequence of to see if the values always determined a Super-Heronian triangle.
satisfying (1). I would then test this sequence of to see if the values always determined a Super-Heronian triangle.
Looking at the three terms, ![]() , my guess was that these values satisfied the sequence given by the recurrence relation
, my guess was that these values satisfied the sequence given by the recurrence relation
| (2) |
I used this sequence to generate more terms, all of which seemed to work (see the table on the next page).
The sequence generated by the recurrence relation (2) can also be represented by
| (3) |
Here are the first terms terms which do, in fact, generate Super-Heronian triangles. The first row generates a line which represents a degenerate triangle.
| a | b | c | Area |
| 1 | 2 | 3 | 0 |
| 3 | 4 | 5 | 6 |
| 13 | 14 | 15 | 84 |
| 51 | 52 | 53 | 1170 |
| 193 | 194 | 195 | 16296 |
| 723 | 724 | 725 | 226974 |
| 2701 | 2702 | 2703 | 3161340 |
| 10083 | 10084 | 10085 | 44031786 |
| 37633 | 37634 | 37635 | 613283664 |
| 140451 | 140452 | 140453 | 8541939510 |
| 524173 | 524174 | 524175 | 118973869476 |
As one can see, the sides get large very fast. It is left to show that every term of the sequence ![]() yields a solution; that is, an area that is an integer. Let
yields a solution; that is, an area that is an integer. Let
![\begin{eqnarray*}
A_n &=& \frac{(2+\sqrt{3})^n+(2-\sqrt{3})^n}{4}\sqrt{3\left[\...
...rac{\sqrt{3}}{4}\left[(2+\sqrt{3})^{2n}-(2-\sqrt{3})^{2n}\right]
\end{eqnarray*}](img22.png)
Let us examine another interesting feature of these triangles. Suppose we use the area formula
![]() . We then have the area of the triangle given by
. We then have the area of the triangle given by
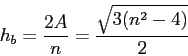
| 1 | 2 | 3 | 0 | - | - |
| 3 | 4 | 5* | 3* | 0 | 4* |
| 13* | 14 | 15 | 12* | 5* | 9 |
| 51 | 52 | 53* | 45* | 24 | 28* |
| 193* | 194 | 195 | 168* | 95* | 99 |
| 723 | 724 | 725* | 627* | 360 | 364* |
| 2701* | 2702 | 2703 | 2340* | 1349* | 1353 |
| 10083 | 10084 | 10085* | 8733* | 5040 | 5044* |
| 37633* | 37634 | 37635 | 32592* | 18815* | 18819 |
| 140451 | 140452 | 140453* | 121635* | 70224 | 70228* |
| 524173* | 524174 | 524175 | 453948* | 262085* | 262089 |
One might observe that the ![]() s can be generated on their own from the recurrence relation
s can be generated on their own from the recurrence relation
Bill Richardson 2010-12-10