I rediscovered an article "Magic Squares and Linear Algebra" by Christopher J. Henrich in the American Mathematical Monthly, Vol 98, no 6, 1991 that has a very interesting 16x16 magic square created by Benjamin Franklin. (There is also an 8x8 magic square from Ben Franklin, but the 16x16 is really fantastic.) Although the diagonals of this square do not sum to 2056, there are many other magical properties. Henrich quotes Franklin as having said, "[it] is the most magically magical of any magic square ever made by any magician."

Note: I entered the square in a spreadsheet and discovered an error in row 2, column 6. The 31 that Henrich has in that position should be 231. The spreadsheet (in Lotus123 WK4) formate can be downloaded for ease in playing with the properties listed below Ben's magic square.

All the rows and columns sum to the number 2056, but that is not all. Half rows and half columns sum to 1028.

The sixteen entries in every 4x4 subsquare sum to 2056.

But there is even more!

In the figures below, the bent diagonals going from top to bottom (Figure 1) sum to 2056. Even the broken ones that have two pieces! Follow the colored patterns and you will be able to check this. (Please forgive the fact that some of the colors look the same. Each bent diagonal or broken diagonal should have 16 cells.) The other three figures show the other diagonals going from from right to left (Figure 2), from bottom to top (Figure 3) and from left to right (Figure 4) also have sums of 2056.

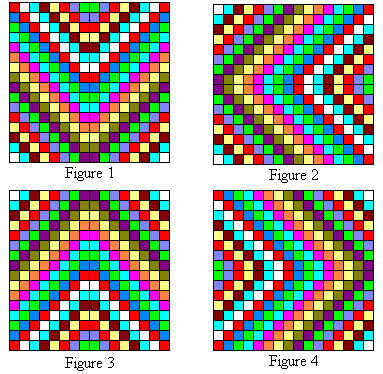
As an example of how to view the bent diagonals, click here for an animation of those in Figure 1.

Please pause for a moment and reflect on the fact that this magic square was constructed over 200 years ago. Even with the aid of a computer this would be a prodigious task.